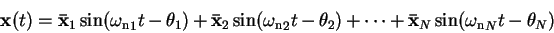pop up description layer
next up previous
Next: Free Response: One Story Up: Introduction to Building Vibrations Previous: Damping Effects

Solutions to the Differential Equations of Motion

In this and the following sections, you will see how the differential equation (12) is solved in three special situations:

  1. the free vibration response to initial displacements;
  2. the vibration resulting from sinusoidal ground accelerations, 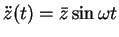; and
  3. the vibration resulting from random ground accelerations.
As in the solution to any differential equation, we will assume a general form of the solution in terms of some unknown constants, substitute this solution into the differential equations of motion, and solve for the unknown constants by plugging in the initial conditions.

Using this standard technique, we will see that in this three story structure, the free vibration of any floor can be represented by the summation of three distinct vibrations, each of different frequency, amplitude and phase. Recall that, in general, any single-frequency oscillation can be represented by an equation of the form

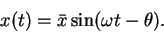(13)
where amplitude is the amplitude, frequency is the frequency of the oscillation in units of radians per second, and phase shift is the phase-shift of the oscillation. This is shown in the figure below:

Figure 4: Mathematical representation of an oscillation.
sinusoidal graph

Remembering also that the matrices are mass- and stiffness-orthogonal and therefore each level can be described separately, we see that
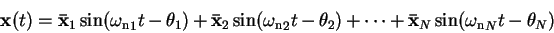(14)

Since describing a three story oscillation is simply the sum of single oscillations, we can first deal with a single story oscillation, and then extrapolate to our multiple story model.

There are many other ways to describe the movement represented by equation (13), and some ways may be more useful for our particular mathematical needs. Before attempting to solve the differential equations in the three situations described above, we will review various ways of denoting sinusoidal motion.

  1. We can rearrange equation (13) in terms of the frequency of the oscillation, represented in cycles per second, or Hertz. (Note that the videos at the beginning of this tutorial and the simulations are labeled Hertz). Alternatively, one could arrange the equation in terms of the period.

  2. Instead of expressing the oscillation in terms of a phase shift, phase shift, the oscillation may be expressed in terms of the sum of a sine and a cosine at the same frequency,
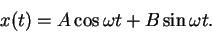    (15)

    This form is equivalent to equation (13) if 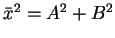and if .

    Trigonometric Identities
    If you need help solving this problem, an external site on trigonometic identities may be helpful.
    After completing this problem, you should see that equations (13) and (15) are equivalent. If not, look again at the page of identities for the difference formula for sine.
    Quick Quiz: What do A and B equal?

    A=x sin theta B=x cos theta
    A=x tan theta B=tan theta/x
    A=tan theta/x B=x tan theta
    A=x cos theta B=x sin theta

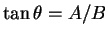  3. A third way of representing this oscillation is through the use of complex numbers:
    position = (16)
      = (17)
      = (18)

    where and complex conjugate of amplitude is the complex conjugate of amplitude.

Note that the equations (13), (15), and (18) are totally equivalent. Taking this complex exponent form one step further, we find that

position = (19)
  = (20)
  = (21)
  = (22)

where 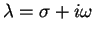. As will be seen in the next few pages, the form of equation (21) is useful in describing damped vibrations. If damping is zero and frequency is not zero, then equation (22) describes un-damped oscillations. If damping is negative and frequency is not zero, then equation (22) represents a sinusoidal oscillation with decaying amplitude as shown in Figure 4 below. Since this is the type of behavior we would intuitively expect to see out of a lightly damped structure, we will use equation (22) as the trial function in the solution of the differential equation (12). While the other ways of describing the oscillations may be more easily interpreted, the mathematical manipulations required to solve the differential equations of motion will be easier if we stick with the form of equation (22).

Figure 5: An exponentially decaying oscillation, a=1.2, b=0.8, damping = -0.2, and frequency = 10.0
graph of an exponentially decaying oscillation

Subsections
next up previous
Next: Free Response: One Story Up: Introduction to Building Vibrations Previous: Damping Effects
Henri P Gavin
2002-03-30