pop up description layer



Next: Free Response: Multiple Stories
Up: Solutions to the Differential
Previous: Solutions to the Differential
Free Response: One Story
To begin to solve equation (12) for a building in free response, let us again consider a one-story structure.
In a structure with a single story, the mass, damping, and stiffness are scalars instead of matrices and the differential equations of motion are
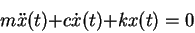 |
(23) |
Assuming sinusoidal motion as described in the previous section, we substitute a trial function of
 , which means that
, which means that
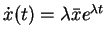 and
and
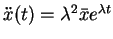 .
Recombining terms in the differential equation of motion leads to
.
Recombining terms in the differential equation of motion leads to
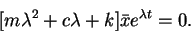 |
(24) |
For equation (24) to hold, either  or
or
 .
The solution
.
The solution  is the trivial solution; the nontrivial solution is
is the trivial solution; the nontrivial solution is
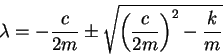 |
(25) |
Assuming no damping in free vibration (c = 0),
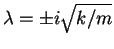 . We see that we are dealing with the natural frequency of oscillation of the system,
. We see that we are dealing with the natural frequency of oscillation of the system,
 , just as we should in analyzing free response.
, just as we should in analyzing free response.
Another special case is when  has a single value, when
has a single value, when
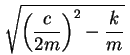 equals zero.
This special level of damping is called critical damping,
equals zero.
This special level of damping is called critical damping,
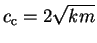 .
It is customary to talk about damping in terms of a fraction of critical damping,
.
It is customary to talk about damping in terms of a fraction of critical damping,
 , where
, where  is called the damping ratio.
We can now rewrite the single-story differential equation (23) and
is called the damping ratio.
We can now rewrite the single-story differential equation (23) and  (equation 25) in terms of
(equation 25) in terms of  and
and  instead of mass, damping, and stiffness:
instead of mass, damping, and stiffness:
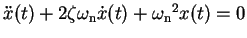 , ,
| (26) |
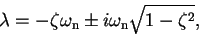 |
(27) |
where we assume here that  .
If the damping ratio is between zero and one, then
.
If the damping ratio is between zero and one, then  will be a complex conjugate pair.
This is called under-damped behavior and is characteristic of oscillatory response.
The imaginary part of
will be a complex conjugate pair.
This is called under-damped behavior and is characteristic of oscillatory response.
The imaginary part of  is called the damped natural frequency
is called the damped natural frequency
 .
.



Next: Free Response: Multiple Stories
Up: Solutions to the Differential
Previous: Solutions to the Differential
Henri P Gavin
2002-03-30
![]() has a single value, when
has a single value, when
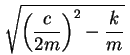 equals zero.
This special level of damping is called critical damping,
equals zero.
This special level of damping is called critical damping,
![]() .
It is customary to talk about damping in terms of a fraction of critical damping,
.
It is customary to talk about damping in terms of a fraction of critical damping,
![]() , where
, where ![]() is called the damping ratio.
We can now rewrite the single-story differential equation (23) and
is called the damping ratio.
We can now rewrite the single-story differential equation (23) and ![]() (equation 25) in terms of
(equation 25) in terms of ![]() and
and ![]() instead of mass, damping, and stiffness:
instead of mass, damping, and stiffness: