An Introduction to Basis Sets:

• energy
• electron density
• electrostatic potential
• transition state (if any)
• frequency

However, calculating MOs is not that easy. The computer, however, does this for us. But, you, the chemist, must tell the computer some information first. Input files for all of the major computational chemistry packages contain these three parts:

1. Geometry which includes
   • Bond lengths
   • Bond Angles
   • Dihedrals
2. Kind of Calculations:
   • Single point energy
   • Frequency
   • Transition state
   • Electron density
   • Electrostatic potential
3. Starting set of mathematics and approximations
   • Calculation method (molecular mechanics, semiempirical, or ab initio
   • Type(s) of approximation (Hartree-Fock, Moller-Plesset, etc.)
   • Basis Set Approximation

The graphic below "captures" the essence of what is the responsibility of the chemist and what is the responsibility of the computer:

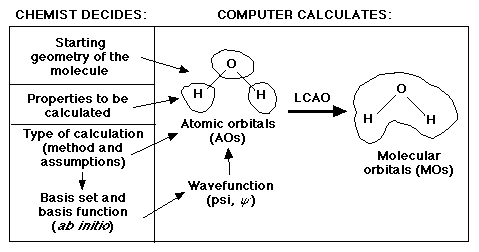
In this lab we will be looking at the third ingredient, basis sets.

A molecular-orbital theory calculation is a mathematical expression of an electron in a molecule. Although there are many types of molecular-orbital functions, in this lab we will only look at the Slater Type Orbitals (STOs) and the Gaussian Type Orbitals (GTOs).

Although there is not a major difference in these two methods when calculating small molecules, major discrepencies arise for larger molecules of 30 or more atoms. STOs require more calculating, which takes tremendous amounts of time, however their calculations have been found to be more accurate than GTOs. On the other hand, GTOs, although less accurate, are much faster to calculate than STOs. This forced scientists to compromise time or accuracy.

Eventually, scientists realized that by adding several GTOs, they were able to mimic the STOs accuracy. In fact, as the number of GTOs used increased, the better they were able to model the STO equation.

When using GTOs to model STOs, the new equations are given a new name. They are identified as STO-kG equations where k is a constant that represents the number of GTOs used. For instance, two common equations are the STO-3G and the STO-6G in which 3 and 6 GTOs are used respectively.