Course Chapters

Calculator Fundamentals

Mathematics Review

Basic Concepts

Advanced Concepts

• Gas Laws
  
• Thermodynamics
  
• Kinetics
  
• Equilibria
  
• Redox Chemistry
  
• Nuclear Chemistry
  

• Basic Matrix Math
  
• Linear Least Squares
  
• Newton's Method
  
• Integration Techniques
  

Pre-test

Post-test

Redox Calculator

Kinetics Arrhenius Calculator

Thermodynamics Calculator

Nuclear Decay Calculator

Linear Least Squares Regression

Newton's Method Equation Solver

Compressibility Calculator

Units Conversion Calculator

Nomenclature Calculator

Texas Instruments Calculators

Casio Calculators

Sharp Calculators

Hewlett Packard Calculators

This half-reaction says that we have solid copper (with no charge) being oxidized (losing electrons) to form a copper ion with a plus-2 charge. Notice that, like the stoichiometry notation, we have a "balance" between both sides of the reaction. We have one (1) copper atom on both sides, and the charges balance as well. The symbol "e-" represents a free electron with a negative charge that can now go out and reduce some other species, such as in the half-reaction:

Here, a silver ion (silver with a positive charge) is being reduced through the addition of two (2) electrons to form solid silver. The abbreviations "aq" and "s" mean aqueous or solid, respectively. We can now combine the two (2) half-reactions to form a redox equation:

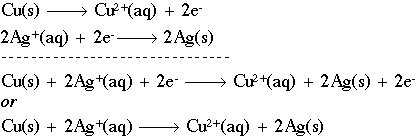We can also discuss the individual components of these reactions as follows. If a chemical causes another substance to be oxidized, we call it the oxidizing agent. In the equation above, Ag⁺ is the oxidizing agent, because it causes Cu(s) to lose electrons. Oxidants get reduced in the process by a reducing agent. Cu (s) is, naturally, the reducing agent in this case, as it causes Ag⁺ to gain electrons.

As a summary, here are the steps to follow to balance a redox equation in acidic medium (add the starred step in a basic medium):

1. Divide the equation into an oxidation half-reaction and a reduction half-reaction
2. Balance these
   • Balance the elements other than H and O
   • Balance the O by adding H₂O
   • Balance the H by adding H⁺
   • Balance the charge by adding e^-
3. Multiply each half-reaction by an integer such that the number of e^- lost in one equals the number gained in the other
4. Combine the half-reactions and cancel
5. **Add OH^- to each side until all H⁺ is gone and then cancel again**

1. For atoms in their elemental form, the oxidation number is 0.
2. For ions, the oxidation number is equal to their charge
3. For hydrogen, the number is usually +1 but in some cases it is -1
4. For oxygen, the number is usually -2
5. The sum of the oxidation number (ONs) of all the atoms in the molecule or ion is equal to its total charge.

Working with redox reactions is fundamentally a bookkeeping issue. You need to be able to account for all of the electrons as they transfer from one species to another. There are a number of rules and tricks for balancing redox reactions, but basically they all boil down to dealing with each of the two half-reactions individually. Consider for example the reaction of aluminum metal to form alumina (Al₂O₃). The unbalanced reaction is as follows:

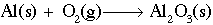Looking at each half reaction separately:

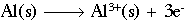This reaction shows aluminum metal being oxidized to form an aluminum ion with a +3 charge. The half-reaction below shows oxygen being reduced to form two (2) oxygen ions, each with a charge of -2.

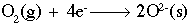If we combine those two (2) half-reactions, we must make the number of electrons equal on both sides. The number 12 is a common multiple of three (3) and four (4), so we multiply the aluminum reaction by four (4) and the oxygen reaction by three (3) to get 12 electrons on both sides. Now, simply combine the reactions. Notice that we have 12 electrons on both sides, which cancel out. The final step is to combine the aluminum and oxygen ions on the right side using a cross multiply technique:

Taking care of the number of atoms, you should end up with:

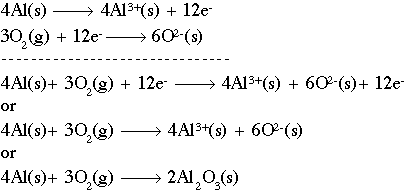
One of the more useful calculations in redox reactions is the Nernst Equation. This equation allows us to calculate the electric potential of a redox reaction in "non-standard" situations. There exist tables of how much voltage, or potential, a reaction is capable of producing or consuming. These tables, known as standard potential tables, are created by measuring potential at "standard" conditions, with a temperature of 298 degrees Kelvin (or 25 degrees Celsius, or room temperature) and with a concentration of 1.0 moles per liter for each of the products. This standard potential, or E⁰, can be corrected by a factor that includes the actual temperature of the reaction, the number of moles of electrons being transferred, and the concentrations of the redox reactants and products. The equation is:

Perhaps the best way of understanding this equation is through an example. Suppose we have this reaction:

In this reaction iron (Fe) is being oxidized to iron(II) ion, while cadmium (Cd) in aqueous solution is being reduced to cadmium solid. The question is: how does this reaction behave in "non-standard" conditions?

The first thing to answer is how does it behave in standard conditions? We need to look at the standard potential for each half-reaction, then combine them to get a net potential for the reaction. The two (2) half-reactions are:

Notice that both half-reactions are shown as reductions -- the species gains electrons, and is changed to a new form. But in the complete reaction above, Fe is oxidized, so the half-reaction needs to be reversed. Quite simply, the potential for the half-reaction of iron is now 0.44 volts. To get the potential for the entire reaction, we add up the two (2) half-reactions to get 0.04 volts for the standard potential.

The question now is: what is the total potential (in volts) for a nonstandard reaction? Suppose again that we have the same reaction, except now we have 0.0100 M Fe²⁺ instead of the standard 1.0 M? We need to use the Nernst equation to help us calculate that value. If you go to the Redox Half-Reaction Calculator, you should notice that the reaction is selected and the appropriate values are entered into the boxes. Since we don't have any species "B" or "D", we have entered zero for their concentrations. The concentration of the solid Fe is 1.0 M (actually, concentrations of solids and solvents (liquids) don't enter into the Nernst equation, but we set them to 1.0 so that the mathematics works out). If you click on the "Evaluate" button, you should learn that the standard potential is -0.44 volts, while the nonstandard potential is -0.5 volts. If you scroll down on the calculator, you can enter 0.5 as the first half-reaction. We again change the sign since we're actually reversing the Fe reaction

Using the calculator again, we calculate the nonstandard potential of the Cd reaction. Suppose we now have a concentration of Cd²⁺ of 0.005 M, what is its potential? The calculator should return a standard potential of -0.4 and a nonstandard potential of -0.47 volts. Place this value in the box for the second half-reaction,then click on "Evaluate". You should learn that the net nonstandard potential is 0.03 volts, slightly less than the value of the net standard potential. Since this value is less than the net standard potential of 0.04 volts, there is less of a tendency for this reaction to transfer electrons from reactants to products. In other words, less iron will be oxidized and less cadmium will be reduced than at standard conditions.

Test your use of the redox calculator by calculating the net standard potential for this reaction:

Answer: 0.025 volts. Since the value is positive, the reaction will work to form the products indicated. Negative values of the potential indicate that the reaction tends to stay as reactants and not form the products. The net standard potential for this reaction is 0.01 volts -- since the nonstandard potential is higher, this reaction will form more products than the standard reaction.

Free energy and the standard potential can also be related through the following equation:

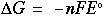Where:

delta G = change in free energy
n = number of moles

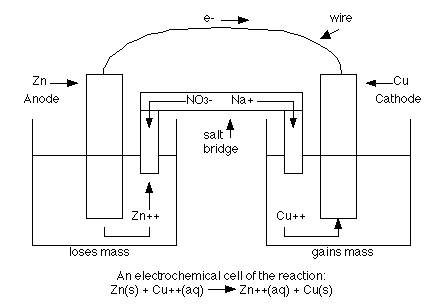
If a reaction is spontaneous, it will have a positive E^o, and negative delta G, and a large K value (where K is the equilibrium constant-this will be discussed more in the kinetics section).

The energy released in any spontaneous redox reaction can be used to perform electrical work using an electrochemical cell (a device where electron transfer is forced to take an external pathway instead of going directly between the reactants. Think of the reaction between zinc and copper. Instead of placing a piece of zinc directly into a solution containing copper, we can form a cell where solid pieces of zinc and copper are placed in two different solutions such as sodium nitrate. The two solids are called electrodes. The anode is the electrode where oxidation occurs and mass is lost where as the cathode is the electrode where reduction occurs and mass is gained. The two electrodes are connected by a circuit and the two (2) solutions are connected by a "salt bridge" which allows ions to pass through. The anions are the negative ions and they move towards the anode. The cations are the positive ions and they move towards the cathode.

The following is a diagram of an electrochemical cell with zinc and copper acting as the electrodes.

An external electric current hooked up to an electrochemical cell will make the electrons go backwards. This process is called electrolysis. This is used, for example, to make something gold plated. You would put the copper in a solution with gold and add a current which causes the gold ions to bond to the copper and therefore coating the copper. The time, current, and electrons needed determine how much "coating" occurs. The key to solving electolysis problems is learning how to convert between the units. Useful information: 1A=1 coulomb/sec; 96,500 coulombs can produce one (1) mole of e^-; the electrons needed is determined by the charge of the ion involved

Example Problem: If you are trying to coat a strip with aluminum and you have a current of 10.0A (amperes) running for one hour, what mass of Al is formed?

The solution of this problem involves a lengthly unit conversion process:

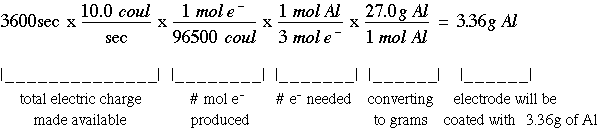
Practice Redox Problem: balance the following redox reaction in acidic solution:

The redox solution is available.

Practice Electrolysis Problem: It takes 2.30 min using a current of 2.00A to plate out all of the silver from 0.250L of a solution containing Ag⁺. What was the original concentration of Ag⁺ in solution?

The electrolysis solution is available.