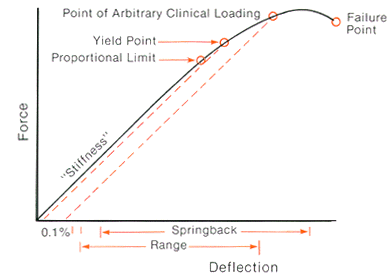
The elastic properties of a material can be expressed in many ways depending on the field of study of the person evaluating the information. Force-Deflection curves are how most people look at elastic properties; however, engineers and orthodontists evaluate elastic properties using the same information in a slightly different manner.

Common Understanding:

As force is applied to an object, it will bend. For a given material, this amount of bending (deflection) is constant. This value is known as the spring constant (k). Their relationship can be expressed in the mathematical equation:

Engineering Understanding:

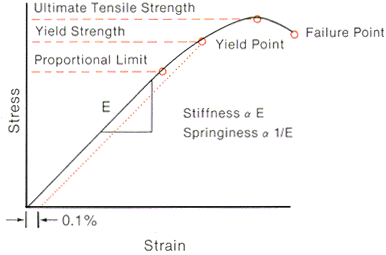
Engineers use the same information with a slightly different application. They look at elastic properties as a relationship of stress to strain. Stress is the internal distribution of the load of the material as defined as force per unit area. Strain is the distortion of the material produced by the externally applied load. It is measured as deflection per unit length. Stress and strain are unique to the material which is being evaluated and have a linear relationship. The line produced by the stress/strain curve has a slope equal to the elastic modulus. Their mathematical relationship is as follows:

Orthodontic Understanding:

• Strength is the quality or state of being strong.
• Stiffness is the quality of being rigid; not easily bent.
• Range is the distance a wire travels before permanent deformation.

Stiffness is the slope of the strength-range graph and is equal to the product of the elastic modulus of the material (E) times its area moment of inertia (I). The value, I, is geometry dependent. Thus, with a change in shape of the same material you will change the stiffness. Let us take a look at a rectangular cross-section versus a circular cross-section.

If you were to double the diameter or height of the object, you will cause a sixteen (16) fold increase in the I of the circle and an eight (8) fold increase in the I of the rectangle. These changes result in a corresponding 16 and 8 fold increases in the stiffnesses.

With the influence of I, you can see how changes in shape and changes in size will affect stiffness.