After designing our model bridge, complete with a gorilla as a load, we now need to see how this gorilla affects the tension and compression of our bridge.
Without any weight on the bridge, we can assume that the tension and compression forces on the members of the bridge are zero. Let's take a look at how this changes with our 100 pound gorilla.
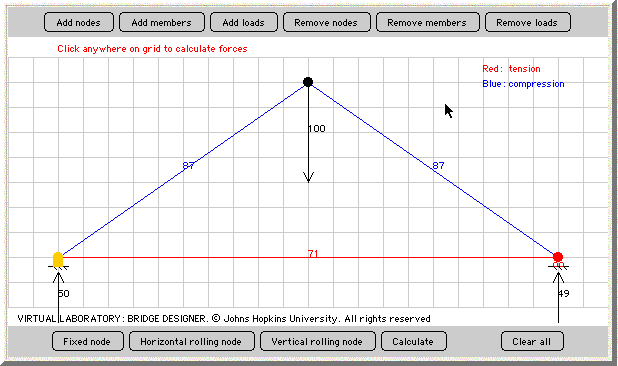
To calculate the tension and compression on the applet, click on "calculate." You will notice that these directions appear in the top left corner.


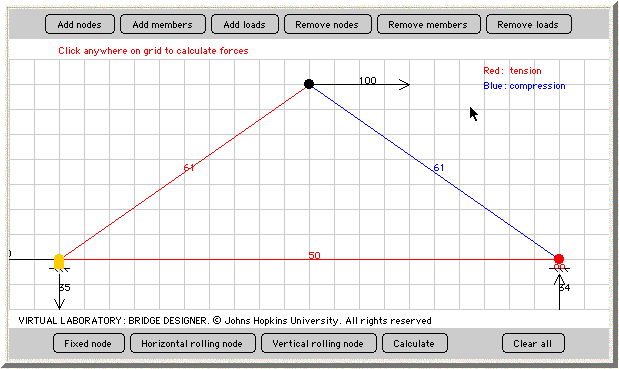
After doing this, you will realize that the members will turns different colors, either red or blue.
The blue represents the members of our bridge that are being compressed, while the red represents the members that are experiencing tension. As the gorilla hangs from our bridge, we find that the side members are being squished and the bottom member is being stretched.
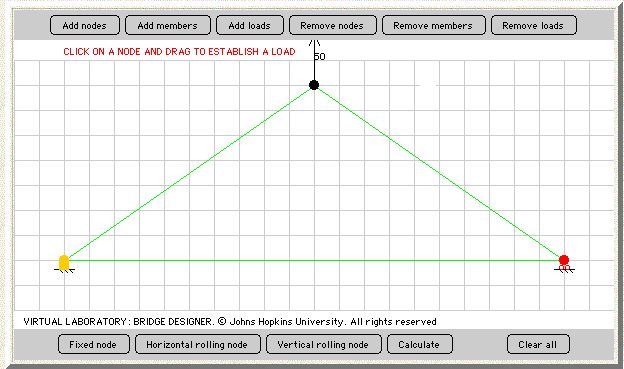
Next, we're going to imagine that we have a 50 pound gorilla that can fly. Instead of hanging from our bridge, this gorilla is going to fly straight up into the air and pull on the bridge from the node.
To delete the previous load, click on "remove loads," then click on the node to which the load is connected to.
Add this next load pointing upwards at 50 units. This load cannot be more than 50 units only because loads cannot continue off the graph. Like in the gorilla hanging down, this model will represent the force our gorilla puts on our bridge when he is flying into the sky and pulling on the bridge.
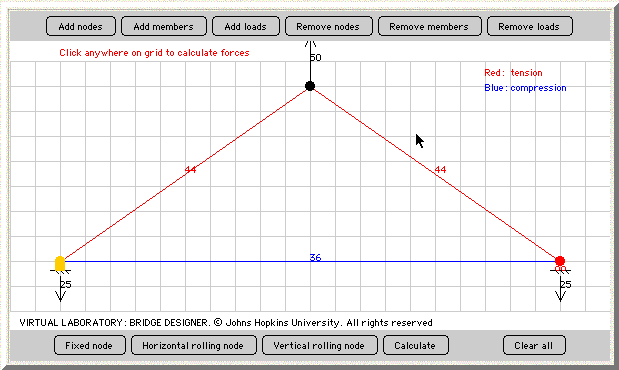
Once again, we need to calculate the forces formed by our flying gorilla. Using the "calculate" button, we find the following results:
Here, we find that the side members are becoming tense, while the bottom member is being compressed. This is the reverse of what we observed in our hanging gorilla model, where the side members were being compressed and the bottom member was becoming tenser. Also notice the values for the compression and tension forces in our flying gorilla model. These magnitudes, or the values of the force, are approximately half the magnitudes of the hanging gorilla model. Why would these values be almost exactly half of the previous model?
Perhaps, you will remember that our flying gorilla was very small in comparison to our hanging gorilla. In fact, he was exactly half the size on our hanging gorilla. As the load is increased or decreased on a simple model like this one, the changes in the magnitudes of the forces of tension and compression will be proportionate to the change in magnitude of the load.
From these results, it would be fairly easy to be able to predict further magnitudes of forces if different loads were added up or down. But, what about a horizontal load? To test this, we will go back to a 100 pound gorilla, but one that flies sideways.
When you do this, be sure to remember to remove the flying gorilla, and add the side load of 100 pounds to the right.
Recalculate the forces that result from the horizontal load.
You will find that the left side of the bridge, which is in the same direction the load pulls experiences tension, while the right side experiences tension. This is similar when the force was pulling down because the member that must push against the force is compressed, while that which must pull is stretched.
The bottom member experiences tension. Why is that? Would it be the same if the load pointed in the other direction? Let's try it. Add a load to the left side of the structure, rather than the right. Don't forget to remove the right load before doing this. Now, calculate. What do you find? Similar to the right load, the left side is compressed, while the right side experiences tension. The bottom member also experiences compression.
Do these results make sense?
Scientists always have to double-check any data that they have received so that they can later explain how they got the data. They also have to be able to answer any questions regarding the validity of the results, as presented by others. This is the only way that theories can later be proven or disproven.
So, do these results of compression and tension in our bridge make sense? We cannot simply assume that the applet is correct because then we would be basing our hypothesis on someone else's hypothesis. Instead, we must understand why we got the results that we did.
Click here to have assistance in determining the validity of our results.
| On to Page 4! |