|
Bob Panoff (Bob1) began the third afternoon session of MEC by having the
students open a spreadsheet in Claris. Bob discussed the associative
property of addition with them, and they did an activity on the computer
to show this property. Also, they demonstrated that the property did
not always apply on the computer due to the computer's roundoff errors.
The class then wondered "How can the computers do complicated equations
like GalaxSee when they can't even do simple math?" Bob1 explained
that the computers have problems with the one problem that he gave them
because computers work in the binary system, and the computer doesn't
use exact fractions because it doesn't have an infinite amount of memory.
The students figured out that this must be a major problem for scientists,
such as physicists like Bob1, using computers to do math. He then went
into a discussion on how many combinations of socks he could get out
of three. The students then began to work out an equation for this.
They then used the same equation to work with GalaxSee. Bob1 then turned
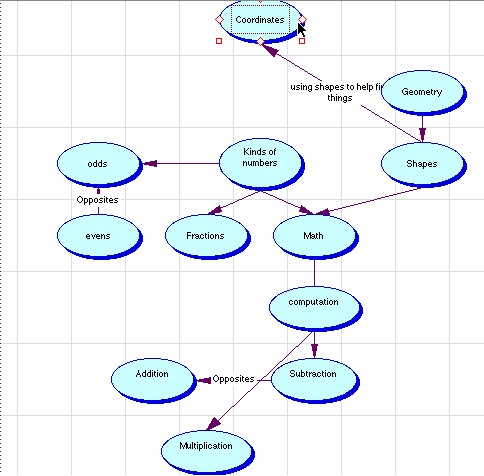
the class over to Maria and Anne. Maria started a game to demonstrate that not all games are fair. In this game, Maria always won. The students then brainstormed other games which were totally unfair. The students then went to a Shodor web site with many math related games like Monty Hall and a maze applet. The students then played the games and wrote down observations on paper. All of the students enjoyed playing the games. After the break the students came in and began discussing the mathematical parts of all these games. They found that things like multiplication, addition, subtraction, probability, angles, and the coordinate plane were involved in the games they played. They then started to play a game where two students were supposedly charged with a huge crime, and they have to figure out whether to confess or not. They played the game with each other, and had a ball. They then tried to determine what the best strategy was. After this was done they discussed the relationships between the math concepts found in games by drawing a concept map.
Last Update: June 24, 1998 Please direct questions and comments about this page to WebMaster@shodor.org © Copyright 1998 The Shodor Education Foundation, Inc. |