CompChem: Reading on Point-Group Symmetry
Reading on Point-Group Symmetry
CompChem Main Page
Symmetry?
In computational chemistry, symmetry is an important property of molecules. Classifying molecules by those properties can be very useful, but it can also be quite complex. This reading will give you an overview of symmetry which will help you interpret the classifications that MacSpartan gives as well as classify molecules on your own. This is not a complete explanation of symmetry, but it covers everything within the scope of this workshop (and then some!).
In this course, we are concerned with only two major symmetry elements: a mirror plane and an axis of rotation. Identifying which combinations of these elements are present in a molecule will enable you to classify the group symmetry.
Symmetry Elements
A symmetry element is some feature of the molecule relative to which an operation can be performed, like rotation around an axis. If the operation gives a result which is indistinguishable from the starting molecule, that element of symmetry is present for that molecule.
- Mirror Plane,
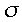
This is what it sounds like, a plane drawn through the molecule so that the molecule is exactly the same on either side of the plane. A more complex way of saying this is that if you invert all of the coordinates in a direction perpendicular to the plane, the resultant molecule is exactly what you started with.
- Axis of Rotation, Cn
This is a line drawn such that rotating the molecule around it by steps of 360/n degrees will result in the same molecule. That is, rotating it n times brings you back to where you started, but at each of the intermediate steps it also looks the same.
Mirror planes are also classified with a subscript of "h" or "v" depending on whether they are horizontal or vertical. Horizontal planes are those which are perpendicular to the axis of rotation, and vertical planes are those which contain the axis of symmetry. These are denoted by 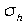 and
and 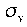 .
.
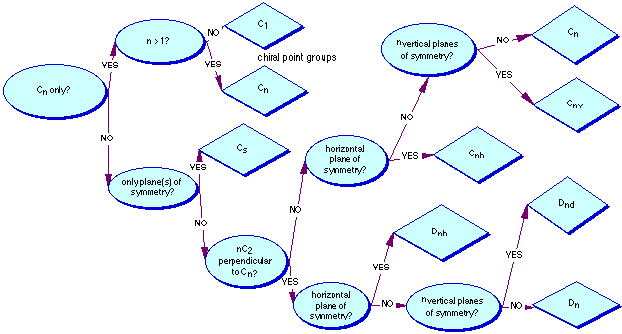
Point-Group Symmetry
The "point-group" symmetry is a method of denoting the combination of symmetry elements which a molecule contains. To use the flowchart below, simply answer "yes" or "no" at every decision box and follow the correct arrow. When you reach a diamond shaped box, that is the point-group symmetry of the molecule.
Which group is benzene (C6H6) in?
Practice with symmetries here
Developed by
 The Shodor
Education Foundation, Inc.
The Shodor
Education Foundation, Inc.
Copyright © 1998
Last Modified:
Questions or comments about this page should be directed to gotwals@shodor.org
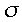
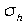 and
and 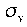 .
.

 The Shodor
Education Foundation, Inc.
The Shodor
Education Foundation, Inc.