Lesson - Angular Solution of Hydrogen Atom

Schrodinger's Equation

Schroedinger's equation applied to a single electron Hydrogen atom takes the following form:

$\begin{displaymath} \mathbf{H} \Psi(\vec{r}) \equiv \left[ -\frac{\hbar^2}{2m}\Delta+V(\vec{r})\right] \Psi(\vec{r}) = E \Psi(\vec{r}) \end{displaymath}$

Written in terms of angular and radial portions, Schrodinger's equation is given by

$\begin{displaymath} \mathbf{H} \Psi(\vec{r}) \equiv \left[ -\frac{p_r^2}{2m}+\fr... ...l}^2}{2mr^2}+V(\vec{r})\right] \Psi(\vec{r}) = E \Psi(\vec{r}) \end{displaymath}$

where

$\begin{displaymath} \mathbf{l} \equiv -i \hbar (r \times \nabla) \end{displaymath}$

Written in terms of the angular variables $\theta$ and $\phi$ , where $\theta$ is the azimuthal angle and $\phi$ is the polar angle (note, many physicists use a different convention where the variables for the polar and azimuthal angles are reversed), the eigenvalue equation for the angular momentum is

$\begin{displaymath} - \hbar^2 \left[ \frac{1}{sin \phi} \frac{\partial}{\partial... ...i} \frac{\partial ^2}{\partial \theta^2} \right] Y = \lambda Y \end{displaymath}$

Azimuthal Term

Noticing that the $\phi$ derivative term does not depend on $\theta$ , and that the $\theta$ derivative term does not depend on $\phi$ , we again separate variables assuming that the solution can be written as

$\begin{displaymath} Y(\phi,\theta) = P(\phi) T(\theta) \end{displaymath}$

In order for Y to be an eigenfunction of the angular momentum equation, T must be an eigenfunction separately of the $\theta$ derivative term in the angular momentum equation.

$\begin{displaymath} - \frac{d^2}{d \theta^2}T(\theta) = \lambda_T T(\theta) \end{displaymath}$

The solution to this is clearly a combination of sine and cosine functions

$\begin{displaymath} T = A cos( \sqrt{\lambda_T} \theta) + B sin(\sqrt{\lambda_T} \theta) \end{displaymath}$

which in its most general form is often written as

$\begin{displaymath} T=e^{i \sqrt{\lambda_T} \theta} \end{displaymath}$

but what values of $\lambda_T$ will satisfy our boundary conditions? What are our boundary conditions?

In this case, T is a function of the angle $\theta$ . Since $\theta$ wraps around the x-y plane, and can have multiple values that correspond to the same angle, our boundary condition is that any solution must work for any two values of $\theta$ that represent the same physical angle.

$\begin{displaymath} T(\theta) = T(\theta + 2 pi) \end{displaymath}$

For what values of $\lambda_T$ will this be true?

Making a polar plot of the sin and cosine functions, it is easy to see that functions where $sqrt{\lambda_T} = m$ and is an integer will satisfy the boundary conditions for the azimuthal angle.

Polar Term

Putting this back into the equation for angular momentum we get

$\begin{displaymath} - \hbar^2 \left[ \frac{1}{sin \phi} \frac{d}{d \phi} \left( ... ...{d \phi} \right) +\frac{m^2}{sin^2 \phi} \right] P = \lambda P \end{displaymath}$

Making the substitution $x = cos \phi$ this can be written as

$\begin{displaymath} - \hbar^2 \left[ \frac{d}{d x} \left( (1 - x^2) \frac{d}{d x} \right) +\frac{m^2}{(1-x^2)} \right] P = \lambda P \end{displaymath}$

While this equation may not have an obvious solution, there are a few things we can see when looking at it.

The equation is not changed if the substitution is made for .

The equation has the potential to have singularities at $x = \pm 1$

We cannot make the assumptions for boundary conditions that we did with azimuthal angle $(T(\theta) = T(\theta) + 2 \pi)$ , nor can we make the assumptions about boundary conditions that we do with the radial solution $y_l(r=0) = y_l(r \rightarrow \infty) = 0$ . We can, however, require that the solution be well defined at $x = \pm 1$ , as the solution must correspond to a physical solution for the wavefunction. It can also be seen looking at the equation that if is not zero, P(-1) and P(1) should be zero, but that if is zero, non trivial solutions can only exist if P(-1) and P(1) are not zero. For m>0, we can make a substitution U = (1-x²) P, and solve the above equation as a system of equations, under the boundary conditions U(-1) = U(1) =0.

A CSERD model of the Legendre Equation exists which numerically solves this equation from near -1 to near 1. (It will display as if it is solved from 1 to 1 because of the tool used to create the model.) This model is being solved for units where $\hbar=1$ . For integer values of , can you modify $\lambda$ to see what values will satisfy our requirement that the equation be physical throughout the range of the function and be either an odd or even function?

The eigenvalues of this equation are often written as

$\begin{displaymath} \hbar^2 l (l+1). \end{displaymath}$

Does this agree with your results?

Like the radial solution for Shrodinger's equation applied to Hydrogen with one electron, this equation also can be solved exactly.

For a derivation of the exact solution, please see MathWorld.

The solutions to the above equation with $\hbar$ set to 1 are referred to as the Legendre Polynomials ().

Solution

Using this solution, and our assumptions about the periodicity of the azimuthal solution, we can write the solution to the angular portion of Schrodinger's equation for a single electron Hydrogen atom as

$\begin{displaymath} \mathbf{l}^2 Y_l^m(\phi,\theta) = \hbar^2 l (l+1) Y_l^m(\phi,\theta) \end{displaymath}$

where

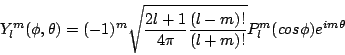
$\begin{displaymath} Y_l^m(\phi,\theta) = (-1)^m \sqrt{ \frac{2 l + 1}{ 4 \pi} \frac{(l-m)!}{(l+m)!} } P_l^m(cos \phi) e^{i m \theta} \end{displaymath}$

and for

$\begin{displaymath} Y_l^{-m} = (-1)^m Y_l^{m *} \end{displaymath}$

The extra terms in the coefficient are strictly for normalization. Nothing in our solution to the equation specified the amplitude of the solutions, so they have been normalized according to standard conventions.

The solution to the angular momentum equation are used often in physics, and are reffered to as the Spherical Harmonics. A description of the Spherical Harmonics can be found at MathWorld, including solutions for the first few terms.

(From: p. 165, Brandt & Dahmen, The Picture Book of Quantum Mechanics, second edition 1995)

Exercises

What does the l=0, m=0 Spherical Harmonic look like? (Consider using the equations from MathWorld and CSERD's 3D Density plot tool. Since you have a function of only two variables, and the 3D plotting tool plots functions of 3, consider multiplying your solution by something that will make the solution drop to zero far from the origin. For example, to plot the 0,0 term, you might use the equation "1/2*1/(sqrt(3.14))*exp(-r)". You may need to increase or decrease the brightness on various plots. Please note that MathWorld uses the convention among physicists for theta and phi, whereas the plotting tool and the equations onthis page use the convention among mathematicians.

l=1, m=0?

l=1, m=1 (real, imaginary, and magnitude (Y^*Y)?)

Higher order terms?