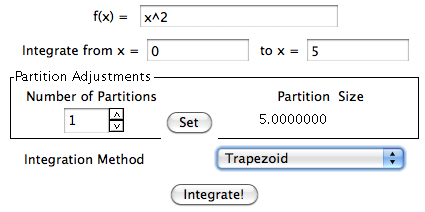
InteGreat
AbstractThe following lesson is designed to introduce students to definite integrals through limits and Riemann sums. This lesson is best implemented in groups of 2-3 students. ObjectivesUpon completion of this lesson, students will:
Standards Addressed:Student Prerequisites
Teacher Preparation
Key Terms
Lesson Outline
Alternate OutlineThis lesson plan can be rearranged in a number of ways:
|