What are Remainders

Student: What are remainders?

Mentor: To see what remainders are, we need to look at division of whole numbers. Suppose we have two numbers X and Y and we want to see how many times X goes into Y. We would use long division, and we would get the number of times X can be divided out of Y -- this is called the quotient -- plus possibly some left over amount if X doesn't divide Y evenly -- this is called the remainder.

Student: So let me try an example. Suppose I want to find out how many times 3 goes into 14. I know 3 times 4 is 12 and 3 times 5 is 15, so I can get 4 threes out of 14 plus some left?

Mentor: That's right. 4 is the quotient and 2 is the leftover, also called the remainder.

Student: This is related to mixed number fractions, isn't it?

Mentor: That is one way we can write the answer to this kind of division. The result of dividing 14 by 3 is 4 with a remainder of 2, or 4 and 2/3 as a mixed number, or 4.666666667 as a 10-digit decimal number.

Try another one.

Student: How about a big one like 67 / 4? Let's see; using my calculator,

How do I get the remainder from this? I don't say 0.75, do I?

Mentor: No, but you have all the information you need. The 16.75 lets you know that 4 goes into 67 sixteen times, so now to find the remainder, just take.

to get the left over. In this case the remainder is 3.

Student: Couldn't I have figured that out from the 0.75? I mean 0.75 times 4 is 3.

Mentor: Yes! That's a good observation. I like the other method better, though, because it works exactly even if the calculator rounds. Try 67 / 7. On my calculator, I get:

What is the remainder here?

Student: I see what you mean. My way, I get

which I could guess means that the answer is 4. Your way I get

Mentor: Either way gets you the right remainder, you just have to remember to "fix" the calculator answer to be a whole number. This process of finding quotients and remainders is called the Euclidean Algorithm after Euclid.

Before we try Coloring Remainders , we need to talk a little more about remainders. Suppose I turn the question upside down: What numbers have remainder X when I divide by Y? Try this: What numbers have remainder 2 when I divide by 3?

Student: Let's see:

Division	Remainder
0/3	none
1/3	1
2/3	2
3/3	none
4/3	1
5/3	2
6/3	none
7/3	1
8/3	2
9/3	none

Neat! I see the pattern. Starting with 2, every third number has remainder 2 again.

Mentor: Very good! Notice that this is true for each possible remainder: 0 (which is what we call "no remainder" situations), 1 and 2 all repeat. Here is a way to remember this -- mathematicians call this idea modular arithmetic. Put your possible remainders in a circle -- this would be all the numbers smaller than your given divisor -- and walk around the circle counting to find the remainder. Try it for a different number, say 5:

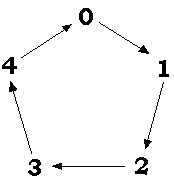
Student: So to find the remainder when 22 is divided by 5, I start at 0 and count. I get to 2 when counting 22 moves around the circle.

Mentor: Does this match our other methods?

Student: Seems to: 22/5 is 4.4 and 0.4 times 5 is 2.

Mentor: This idea comes in very handy in advanced mathematics. It is so common that terminology was invented to ask this question concisely. When we want to find the remainder that occurs when 22 is divided by 5, we ask: What is 22 mod 5?.

Try one more: What is 8 mod 5?

Student: I like the circle, so I'll do it that way. Counting moves around gets me to 3, so 8 mod 5 is 3.

Mentor: Good!