Finding the Volume of a Triangular Prism
|
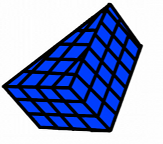
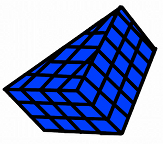
Student 1: How can we find out how much a three dimensional object can hold inside (its volume)? Mentor: Well, there are different methods for finding volume depending on the three dimensional shape. Let's look at a three dimensional triangular shape. How do you think we should solve for the volume of this shape? Student 2: Well, to find the area of a flat triangle we would multiply one half times the base length times the height. Maybe we do something like that to find the volume of a three dimensional triangle shape? Mentor: Good thinking! You are very close. A flat shape is called a two-dimensional shape because it has two dimensions (in the case of a triangle they are often called base and height) while a three dimensional shape will have three dimensions. Let's look at a three dimensional triangular shape (a triangular prism):
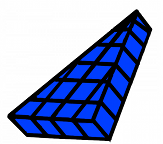
This shape has a base width and a base height (we will call this the base depth) just like you mentioned flat triangles having, but what else does a three dimensional shape have that flat shapes don't? What is the extra dimension? Student 2: There is another side that shows you how high it is. Mentor: Right! This is called the prism height! The prism height is what makes this a three dimensional figure since there are a total of three dimensions: base width, base depth, and prism height! All of these dimensions are used to find the volume of a triangular prism. To find the area of a two dimensional triangle we multiply one half of the base width by the base height so lets start with finding the area of a two dimensional part of the triangular prism. We will first look at the top layer of the triangular prism when there is base width and base depth but no prism height.
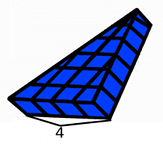
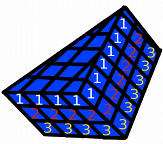
Mentor: What is the base width of this shape? Student 1: 4! There are four full cubes along the base of the triangle.
Mentor: Great, so the base width is 4 units, now what is the base depth of the triangle? Remember, base depth is the distance from the middle of the base to the top point of the triangle (the apex). Student 2: The base depth is 6 units! There is a length of six cubes from the base of the triangle to the top of the triangle.
Mentor: That is right! Now we can find the area of this flat triangular shape. What do I do to find the area? Student 2: You multiply 1/2 to the base width (4) to the base depth (6). The answer is 12 units! Mentor: Correct! Now, we haven't found the volume yet, what are we missing? Student 1: We need to include the prism height! Mentor: Right, let's take another look at our three dimensional shape:
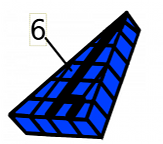
Mentor: See the flat triangular shape we looked at is only one layer of this big shape. Think about it like this: the flat shape that we just looked at is stacked on other shapes identical to itself. How many of the flat shapes are stacked up in this 3 dimensional figure? Student 2: Well, there is one layer on the top, another layer of the same shape below it, and then the layer that is on the bottom. There are 3 layers total!
Mentor: Great job. The number of layers represents our prism height! Student 1: So our third dimension, prism height, is 3 units? Mentor: Yes. Now, knowing that in the three dimensional shape there are three layers of the flat shape we looked at, and knowing that the flat shape has an area of 12 square units, how do you think we will find the volume? Student 2: If there are three layers, each with an area of 12 square units, we can add 12+12+12 and that will give us the total volume! Student 1: We could also multiply the area of the flat shape, 12, by 3. That is the same thing as adding an area of 12 three times. Mentor: Right! And what do you get when you multiply 12 by 3? Student 1: 36! The volume of the three dimensional object is 36 cubic units! Mentor: Great job! You found the volume of a triangular prism. Here are the steps that we took to find our answer:
Mentor: So, in order to find the volume of a triangular prism we multiply 1/2 by base width by base depth by prism height. |