Introduction to Cryptography: Shift Ciphers
Suppose that we created a "clock" that had 26 numbers on it. We could match every number to a letter. Then what could we do to "encode" the message?
Have the class "shift" the cipher by adding a constant to each letter's numeric value. For an example, let's have a constant of 5. In this case, A=0. Add 5 to that, to get 5. Convert that back to a letter, 5=F.
So that's what happens with A, but what about Z? Z=25. Let's add 5 to that to get 30. And now we convert back into letters to get... wait, what is 30?
Here's where we get into the "modular arithmetic" part. Does anybody know how modular arithmetic
might help us with this? Consider the following alphabet wheel:
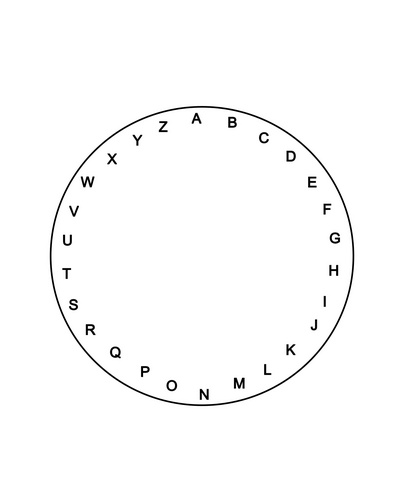
You can just keep going around the wheel. So Z would end up being E.
With a constant of 5, the message "I really like code messages" is encoded to be the following:
N WJFQQD QNPJ HTIJ RJXXFLJX
And in cases like this, it's really easy to see to just keep going around the wheel like that. But suppose through the course of encoding the letter, it became 136 instead of a smaller number like 30 from the previous example. How would we know what the new letter would be in this case?
Through modular arithmetic, of course! What's 136 mode 26? 6. So Z would be G in this cipher.