In Straws We Trussed - Page 4
REVERSE LOAD
To change the scenario, we will give the gorilla a rocket pack, so that instead of hanging from our bridge, this gorilla is going to fly straight up into the air and pull on the bridge from the node. The rocket pack with the gorilla attached can exert a constant vertical lifting load of 50 pounds.
Add this new load pointing directly upwards at 50 units. (This load cannot be much more than 50 units because loads cannot continue off the graph). Like in the gorilla hanging down, this model will represent the force our gorilla puts on our bridge when he is flying into the sky and pulling on the bridge.
Once again, we need to calculate the forces formed by our flying gorilla. Using the "calculate" button, we find the following results:
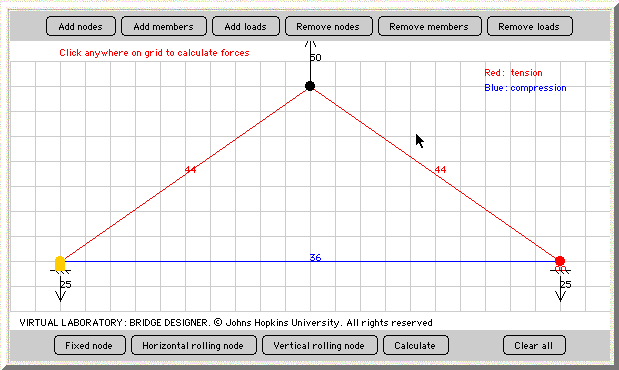
Here, we find that the side members are in tension, while the bottom member is in compression. This is the reverse of what we observed in our hanging gorilla model. Also notice the values for the compression and tension in our flying gorilla model. The magnitudes of these internal forces are approximately half the magnitudes of the forces in the hanging gorilla model. Why would these values be almost exactly half of the previous model?
Remember that in addition to pulling in the opposite direction, our flying gorilla also exerted less load than our hanging gorilla. In fact, the upward load was exactly half the size of the downward load. In trusses, if the load is increased or decreased in the same direction or in the exactly opposite direction, the magnitudes of the resulting reactions as well as the tension and compression in the members will be proportionate to the magnitude of the load.
From these results, it would be fairly easy to be able to predict further magnitudes of forces if different loads were added up or down. For example, what would you expect would occur if the load at the top node was 25 units (i.e. one quarter of the original hanging gorilla load) directly DOWN? Which members would be in tension? in compression? What would the magnitude of the internal forces in each member be? What would the reactions be? Record your predictions and then test them by removing the 50 unit load and adding the 25 unit downward load.
| On to Page 5! |