In Straws We Trussed - Page 3
TENSION AND COMPRESSION IN A TRUSS
After designing our model bridge, complete with a gorilla as a weight, we would now like to see how this force affects the tension and compression of our truss bridge. To calculate these effects click on the 'Solve' button. Then the model should run.

When you do so, you should see some changes to the truss. In particular, the members will turns different colors, either red or blue, and additional force arrows will appear at the supports.
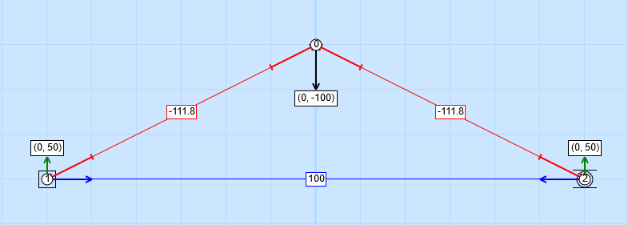
The force arrows that appear at the supports are the reactions and show how much force the supports are exerting on the truss. The reactions should be 'equal and opposite' to the forces, which in this case is almost true - the sum of the left reaction and right reaction (50 + 49 = 99 in an UPWARD direction) is almost equal to the 100 pound weight in the DOWNWARD direction. This actually brings up a very important point about computer programs. ALL computer programs/calculators/etc. have the potential of making very small errors when they do math and can give numbers that are not perfect as output. It is up to the scientist to determine whether the computer is wrong or whether it is making very small errors. In this case, the applet only displays whole numbers and for the support on the right, it probably calculated a number like 49.99999998, which is very close to the correct value of 50, but it only displayed the '49'. Now that we have noticed this for this applet, we will expect our results to possibly be off by 1 unit when we use this program.
The blue represents the members of our bridge that are under compression, while the red represents the members that are experiencing tension. As the gorilla hangs from our bridge, we find that the side members are being squished and the bottom member is being stretched. The numbers next to the members measure how much tension or compression there is. Notice that these numbers do NOT add up to be equal to the forces! In order for the two side members to hold the gorilla up between them, they must each hold 87 pounds of compression. This is because they are pushing at an angle, and must push horizontally against each other as well as vertically to hold up the gorilla.
Note how the truss behaves under a force that pushes DOWN in the middle and support reactions that push UP on the ends. The members along the TOP are in compression and those along the BOTTOM are in tension. This is the same as the foam beam in bending.
Next, we're going to change the load and see how it affects the condition of the members. To delete the previous load, click on "Delete" button, then click on the node to which the load is connected to.

| On to Page 4! |