Chaining Nature down with Mathematics: the Roothan and Schrodinger equations.

A paper by C. Brent Bettini, North Carolina School of Science and Mathematics, Durham NC. Completed as a part of the the Computational Chemistry Seminar Series

< a href="../index.html">Comp Chem Main Page Shodor Home Page

SECTION 1: AN INTRODUCTION

Nature is an interesting and complicated set of order and chaos. Since the awakening of mathematics and science, mankind has strived to describe nature in a general way: equations. The idea is simple; take all the variables in a system, crunch them through some combination of functions and operators, and get an answer that describes what you want to know. Those that accomplish the task of describing nature mathematically have engraved their name on the tablets of history. We all know who they are: Plato, Archimedes, Pythagoras, Newton, Kepler, Galileo, Descartes, Planck, Einstein, Hawking, and many others. For the majority of these accomplished people, they have excelled in physics, mechanics, or pure mathematics. The field of quantum chemistry, down in the realm of ab initio, however, has yielded few who have branded their names on history. Nonetheless, some have met the challenge in quantum mechanics, most noteably Roothaan and Schrödinger, whose work is the subject of my research. To describe nature subjectively is not easy, but to constrain nature within objective equations is nearly impossible. This near impossiblity, and how it was achieved on the quantum scale, is the focus of this treatise.

Our discussion should first concern the division of equations in the realm of ab initio. On one hand there is the Roothaan equation, FC=SC, whose existence is based on knowing extremely large matrices of information. F is the so-called Fock operator, whose derivation is pursued in Section 3, C is matrix defining the expansion coefficients of the system, and is a diagonal matrix of orbital energies; derivation of the entire Roothaan equation itself will be explored in the next section. Schrödinger's equation, however, is a bit more chained down and proves easier to use when calculating unknowns. Schrödinger's equation is defined as H=E, where H is a Hamiltonian operator describing how one wants the , which is contained in Hilbert space, restricted, so that useful and pertinant information can be extracted. E is defined as the total energy of the system, kinetic plus potential energy (KE + PE).

Ab initio equations like Roothaan's and Schrödinger's equations, are used to determine properties of molecules; indeed, that is the only reason for having these equations around and performing the extensive calculations. Properties of the molecules are determined via the wavefunction, , which is an eigenfunction of all ab initio formulas. Wavefunctions are important sets, or matrices, that give information about every possible situation occuring within a molecule. Ab initio equations do not allow us to find specific data about a molecular system directly, but they do provide us a method for calculating the wavefunction, which is the only piece of information we need to know about a molecular system.

Today, with an idea of the magnitude of these wavefunctions (which often times are vectored for Hilbert space at some point in their lifetime), quantum chemists employ computers to solve the tremendous calculations necessary for both the Roothaan equation and Schrödinger's equation. Desktop computers, such as PC's and Macintosh's are only useful on the very smallest scale; one could expect to, at most, calculate bond energies for the first few hydrogenic atoms, up to around Beryllium, depending on the processor. Much more useful to the solution of these equations is the supercomputer, such as the Cray, and even smaller scientific workstations can be used for quantum calculations. With an idea of the magnitude of the calculations involved in ab intio calculations, let us take a closer look at the most complex equation of them all: the Roothaan equation.

SECTION 2: The Roothaan equations.

The Roothaan equations begin with a spatial integro-differential equation, known as the fundamental Roothaan Equation 1:

(1) f(r1)i(r1) = ii(r1)

Let's dissolve this equation into its parts. Firstly, i, is the wavefunction describing the molecular orbital. f(r1) is the Fock operator, which is a function that, given a specific r (r is the electron family function), manipulates and restrictes the system and removes the system from Hilbert space. Finally, i is a diagonal matrix of orbital energies. The index "1" tagged onto the r indicates the one-electron family of functions, and the "i" on and represents the number of basis sets taken into account, which, to obtain a precise answer, would be infinity.

From this fundamental equation, Roothaan was able to show that by introducing a set of K known basis sets, the spacial integro-differential equation (1), could be reduced to a set of matrices and algebraic equations that could be solved by standard matrix techniques.

Therefore, we introduce a set of K known basis sets. These basis sets manifest themselves in the linear expansion of i and form the second-order Roothaan equation:

(2)

As you will notice, equation (2) is the general form used for calculating energies associated with molecular orbitals in the Linear Combination of Atomic-Molecular Orbitals theory. Instead of letting K approach infinity, and thus place the formula in Hilbert space, Roothaan is limiting the basis set, so as to simplify calculations. Again, i, is the i-th molecular orbital, Ci is the i-th coefficient of linear combination, and is the -th atomic orbital, and of course K is the number of atomic orbitals, or basis sets, we wish to consider. Substitution (eq. 2 into eq. 1) and simplification (replace with v) yields:

(3)

Roothaan still had not succeeded in reducing this differential-summation into a algebraic matrix equation. The next step, in order for the reduction to take place, requires the multiplication of the summation differential above with *(1) and singly-integrating, yielding:

(4)

Not much simpler, you say? Well, actually (4) is precisely where we want to be. If we define two K x K Hermitian matrices, which are characterized by the ability to be diagonalized by a unity matrix, we reduce our calculation load significantly:

The overlap matrix, S:

(5)

The name overlap is derived from the interaction of the {} basis functions, which are assumed to be normalized (the integration of the basis function should have normalized the set from zero to one) and linearly independent. The basis functions are not, in general, orthogonal to each other, and tend to have common values. The amount of this overlap, or common values, is derived by normalizing

By the definition of a Hermitian matrix, we see that the diagonal of this matrix is unity (that has a value of one) and all off-diagonal elements are less than one, with the edges approaching zero.

The Fock matrix, F:

(6)

The Fock matrix is an important element of the Roothan equation. This matrix is the array representation of the Fock operator, for the set of basis functions, {}.

Now that we have defined the two matrix portions of equation (4), we can rewrite (by substitution), the equation as:

(7)

which after even more simplification yields, FC = SC. is still a matrix of orbital energies, of the form:

C is a K x K square matrix of all the expansion coefficients of the system, which takes on the form: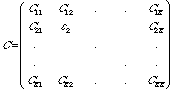

To find the solution to each of the unknown elements in the general Roothaan equation, FC = SC, we turn our attention to Section 3: Solution to the Unknowns.

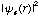SECTION 3: Solutions to the Unknowns.

Given that an electron has a probability of being located at a given point in a volume by the spacial wavefunction

, we can say that a closed-shell molecule that is described by a single wavefunction, with two electrons in each molecular orbital, has a total charge density of:

(8)

If one were to integrate equation (8), the result would be just the total number of electrons, N. Given equation (8), and replacing the wavefunction operand, 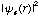, with the equivalent represented by the molecular orbital expansion, equation (2):

(9)

where we have defined as a density-matrix of the form:

(10)

From equation (9) we see that the matrix completely defines the charge density, (r), for a given set of basis functions. By equation (10), we see that Pv is defined in terms of the expansion coefficients, matrix C, so we can, in general, say that the matrix C can be represented by either a measured set of C, or by the matrix . With the representation of the expansion coefficients, C, out of the way, we attenuate our senses to the particular solutions and an expression for the Fock matrix, M.

As was said earlier, the Fock matrix is a matrix representation of the Fock operator:

(11)

which, when represented within the K known basis set {}, expand to:

(12)

where the core-Hamiltonian is defined as:

(13)

The elements of the core-Hamiltonian are integrals describing the nuclear attraction and kinetic energy of an electron. While the calculation of the Fock matrix is impossible without knowing the elements of the core-Hamiltonian (i.e. h(1)), the calculation of the Fock matrix is impossible. The reader should refer to additional text for this information, as it is not within the scope of this research.

After calculating the nuclear attraction integral and kinetic energy integral of the core-Hamiltonian, and substituting again equation (1), the Fock matrix becomes represented by:

(14)

This is the expression for calculating the Fock matrix. The one-electron set is H, which is fixed and calculable by the core-Hamiltonian. G is a two-electron part which can be derived by a combination of the density matrix (equation (10)) and a bi-electron integral:

(15)

A small editorial note about this calculation. Solving for the Fock matrix is not a difficult task in itself. However, the large volumes of calculations make only the most efficient and quickest computer a plausible source for these calculations. For instance, take the outer realm of ab initio, a basis set of about 100 (K = 100). With this number of basis sets, there are 12,753,775 unique integrals that must be solved in order to find the Fock matrix!

SECTION 4: Calculation of the Wavefunction by the Roothaan Equation.

We have seen that the Fock matrix is dependent upon the charge density of the system, that is F=F(P), or similarly dependent on the expansion coefficients, i.e., F=F(C). This dependence on the charge density or expansion coefficients makes the Roothaan equation non-linear, or non-functional: F(C)C=SC

The Roothaan equation's non-functionality makes solution only possible by iteration. At each iteration the Roothaan equation, FC=SC, is reevaluated with the previous, more refined value, similar in fashion to Euler's method of functional approximation. The equation can not be solved directly, in most cases, because S is not a unit matrix, that is, it is not orthonormal to the basis set. If S were a unit matrix, then the Roothan equation could be written as FC=C, which could be solved by diagonalizing F, and calculating the eigenvectors C and eigenvalues . To normalize S (make S orthonormal) is also beyond the scope of this text, and the reader should consult other authorities for information relating to the normalization process.

Normalization of the S matrix gives us three important equations that are necessary for the solution of the Roothaan equation:

(18)

The Roothaan equation can now be solved, with transformation equations (16) to (18). C' can be found by diagonalizing F'. C can then be calculated by using C' in (16), as well as can X. With X known, F can be calculated by (17). Once F is known, we can solve the Roothaan equation for C and .

That is it! The Roothaan equations have now been solved, and we have gained a better mathematical understanding of nature's order and chaos. Actually, the Roothaan equations begin as a set of partial differential equations. For simplicity, the calculations involved in transforming the fundamental Roothaan equation have been omitted from this research. As a point to make, however, the result of these calculations make the fundamental Roothaan equation spin-independent.

Developed by
Graphic of Shodor Logo