Following a Reaction Path with Gaussian 94

Gaussian94 uses the IRC keyword to study reaction paths. The following description from the Gaussian94 users guide is useful:

IRC
This method keyword requests that a reaction path be followed. The initial geometry (given in the molecule specification section) is that of the transition state, and the path can be followed in one or both directions from that point. The forward direction is defined as the direction the transition vector is pointing when the largest component of the phase is positive.
The geometry is optimized at each point along the reaction path. (...)
IRC calculations require initial force constants to proceed. You must provide these to the calculation in some way. The usual method is to save the checkpoint file from the previous frequency calculation (used to verify that the optimized geometry to be used in the IRC calculation is in fact a transition state), and then specifiy IRC=RCFC in the route section. (...)
IRC calculations accept Z-matrices and Cartesian coordinates as molecule specifications.

Path Selection Options
Forward: follow the path only in the forward direction, where "forward is defined as the direction the transition vector is pointing when the largest component of the phase is positive.
Reverse: follow the path only in the reverse direction.
MaxPoints=N: number of points along the reaction path to examine (in each direction if both are being considered)
StepSize=N: step size along the reaction path, in units of 0.01 a.u.
MaxCyc=N: sets the maximum number of steps in each geometry optimization. The default is 20.

Coordinate System Selection Options
MassWeighted: follow the path in mass-weighted internal coordinates. MW is a synonym for MassWeighted. This is the default
Internal: follow the path in internal (Z-matrix) coordinates. Cartesian: follow the path in Cartesian coordinates.

Needless to say, computations of reaction pathways are multi-part processes. You have the option of doing each part of the computation as a single job, or you can run all parts together as one job using some the Link options that were described in the geometry optimization reading. Fundamentally, reaction pathway analysis is a three step process:

determine the optimized geometry of the transition structure
ensure that you have a transition structure by characterizing the stationary point using a frequency calculation.
run the IRC calculation

An example of how this might work is shown below. We'll revisit the formaldehyde molecule. One of the reaction pathways that formaldehyde takes is its dissociation to CO and H₂. What is the activation energy for the reaction? By calculating the energies of the reactant and two products, and the energy of the transition structure, we can easily calculate its activation energy.

The first step is to run an optimization of the transition state. One possible transition state might be the hydrogen elimination to give H₂ and CO. Hehre ("Ab Initio Molecular Orbital Theory") describes the reaction as follows:

The elimination reaction

                H₂CO ---> H₂ + CO

has also been investigated.  Least-motion removal of H2 from formaldehyde, 
while retaining C_2v symmetry is forbidden by orbital symmetry 
considerations;  the true transition structure (below) distorts to 
Cs symmetry:

                                 C----O
                                / \
                               /   \
                              H-----H

One guess for a transition structure would be the breaking of one of the bonds in the C=O carbonyl, as shown above. By virtue of breaking this double bond, we increase the size of the O-C-H bond angle. We will need to try to come up with some logical guess as to the size of this angle. There is some danger that, depending on the angle chosen, when we try to optimize this structure, we'll converge to an angle at or greater than 180 degrees, at which point Gaussian94 complains I have a dummy variable, X, as shown:

In this case, we're going to replace the broken bond with a dummy atom. A separate reading on dummy atoms is included in this session, and unless you have experience with technique, it will be worth your time to read it. The dummy variable in effect breaks one of the C-H bonds, and should allow us to account for all of the electrons. This puts the O1-C2-H4 angle somewhere around 156 degrees -- you can use whatever bond angle there you feel comfortable with. Dividing this in half gives the O1-C2-X3 and O1-C2-H4 bond angles at 78 degrees. In the input file shown below, I begin by requesting that the checkpoint file be saved as H₂CO I've requested this run at a 6-31G level, which is a pretty high level in terms of computational complexity. You may wish to choose a minimal basis set, such as STO-3G, for preliminary runs. In the routing section, an optimization is requested. The CalcFC option requests that the initial force constants be calculated, rather than guessed. As you might suspect, this is more computationally expensive, but substantially more accurate. The TS option requests that the optimization proceed to a transition state rather than to a local minimum.

%Chk=H2CO
# RHF/6-31G Opt(CalcFC,TS) Test
 
H2 + CO <-> H2CO (Opt)
 
0,1
 O
 C,1,R2
 X,2,1.,1,A3
 H,2,R3,3,A3,1,180.
 H,4,R4,2,A4,1,0.
      Variables:
 R2=1.20
 R3=1.13
 R4=1.00
 A3=78.
 A4=85.

Even though we are fairly certain that this is a valid transition state, it is important to characterize the stationary point found in the optimization of the transition geometry. It is here that a frequency calculation is used. We can save computing time by using the force constant values and the optimized geometry calculated by the optimization run through the use of the Guess=Read and Geom=Checkpoint keywords. As mentioned in the previous section, it is important to always use the same basis set throughout the run.

%Chk=H2CO
# RHF/6-31G FREQ Guess=Read Geom=Checkpoint Test

H2 + CO <-> H2CO (Freq)

0 1

Remember that you still must include the charge and multiplicity, followed by a blank line. The molecular geometry specification is being retrieved from the checkpoint file.

The output for this section shows one imaginary frequency:

******    1 imaginary frequencies (negative signs) ******
 Harmonic frequencies (cm**-1), IR intensities (KM/Mole),
 Raman scattering activities (A**4/AMU), Raman depolarization ratios,
 reduced masses (AMU), force constants (mDyne/A) and normal coordinates:
                     1                      2                      3
                    A'                     A'                     A"
 Frequencies -- -2185.2500               781.7490              1044.2087

Remember that you can look in the job archive at the end of the run, to see if NIMAG is set to 1, which is the number of imaginary frequencies:

Test job not archived.
 1\1\NCSC-FLYER\Freq\RHF\6-31G\C1H2O1\TNG60\17-Aug-1995\0\\# RHF/6-31G
 FREQ GUESS=READ GEOM=CHECKPOINT TEST\\H2 + CO <-> H2CO (Freq)\\0,1\O,-
...stuff deleted
 ]\NImag=1\\0.03513009,0.,0.01984599,0.04205894,0.,1.09716234,0.0036780

At this point you are ready to run the IRC calculation. Again, we can reduce computational time by getting many of the input values from the checkpoint file. The RCFC option, if you recall, gets the Cartesian coordinates from the frequency calculation.

%Chk=H2CO
# RHF/STO-3G IRC=RCFC Guess=Read Geom=Checkpoint Test

H2 + CO <-> H2CO (IRC)

0 1

The output from this run looks very similar to that of an optimization run:

IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC-IRC
 ------------------------------------------------------------------------
                         Z-MATRIX (ANGSTROMS AND DEGREES)
 CD Cent Atom  N1     Length/X     N2    Alpha/Y     N3 
    Beta/Z      J ------------------------------------------------------------------------
   1   1  O     0  -0.134614          0.000000         -0.682568
   2   2  C     0  -0.134713          0.000000          0.461888

Here you see the line "IRC-IRC-IRC", followed by the various input geometries and calculations. IRC calculations then provide you with a table of results:

----------------------------------------------------------------------
                 SUMMARY OF REACTION PATH FOLLOWING:
                 (Int. Coord:  Angstroms, and Degrees)
 ----------------------------------------------------------------------
  
           		ENERGY	  RX.COORD    X1       Y1	Z1           
           1         -113.65874  -0.59922  -0.14757   0.00000  -0.68561
           2         -113.65061  -0.49923  -0.14623   0.00000  -0.68535
           3         -113.64358  -0.39924  -0.14493   0.00000  -0.68507
           4         -113.63783  -0.29926  -0.14366   0.00000  -0.68477
           5         -113.63354  -0.19927  -0.14243   0.00000  -0.68447
           6         -113.63085  -0.09928  -0.14125   0.00000  -0.68417
           7         -113.62988   0.00000  -0.14008   0.00000  -0.68387           
           8         -113.63087   0.09940  -0.13898   0.00000  -0.68356
           9         -113.63369   0.19938  -0.13798   0.00000  -0.68329
           10        -113.63833   0.29937  -0.13705   0.00000  -0.68305
           11        -113.64471   0.39936  -0.13618   0.00000  -0.68285
           12        -113.65268   0.49935  -0.13537   0.00000  -0.68269
           13        -113.66199   0.59934  -0.13461   0.00000  -0.68257
                     
           		X2	  Y2	 	Z2	  X3	  Y3           
           1           -0.06787   0.00000   0.48192  -0.00978   0.00000
           2           -0.07434   0.00000   0.48038   0.03114   0.00000
           3           -0.08067   0.00000   0.47884   0.07274   0.00000
           4           -0.08685   0.00000   0.47731   0.11497   0.00000
           5           -0.09288   0.00000   0.47576   0.15780   0.00000
           6           -0.09872   0.00000   0.47418   0.20124   0.00000
           7           -0.10462   0.00000   0.47250   0.24701   0.00000           
           8           -0.11030   0.00000   0.47077   0.29332   0.00000
           9           -0.11556   0.00000   0.46907   0.33826   0.00000
           10          -0.12061   0.00000   0.46732   0.38362   0.00000
           11          -0.12547   0.00000   0.46553   0.42930   0.00000
           12          -0.13016   0.00000   0.46373   0.47520   0.00000
           13          -0.13471   0.00000   0.46189   0.52126   0.00000
                          
           		Z3	  X4	 	Y4	  Z4           
           1            1.53741   1.43952   0.00000   1.01408
           2            1.53383   1.45431   0.00000   1.03186
           3            1.52957   1.46734   0.00000   1.04991
           4            1.52488   1.47859   0.00000   1.06822
           5            1.52002   1.48802   0.00000   1.08678
           6            1.51524   1.49548   0.00000   1.10554
           7            1.51065   1.50135   0.00000   1.12525
           8            1.50666   1.50514   0.00000   1.14907           
           9            1.50357   1.50696   0.00000   1.16412
           10           1.50161   1.50694   0.00000   1.18313
           11           1.50072   1.50535   0.00000   1.20202
           12           1.50099   1.50246   0.00000   1.22074
           13           1.50244   1.49866   0.00000   1.23927
 ----------------------------------------------------------------------
  TOTAL NUMBER OF GRADIENT CALCULATIONS:     26
  TOTAL NUMBER OF POINTS:     12
  AVERAGE NUMBER OF GRADIENT CALCULATIONS:   2.16667

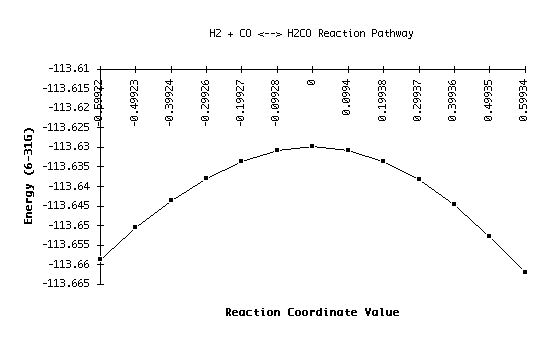
The items are shown in order of increasing distance along the reaction coordinate. For example, structure 1, with an energy of -113.65874, represents the dissociated side of the reaction. The transition state, or top of the barrier, can be identified where the reaction coordinate is equal to zero; in this data set, that puts the energy at -113.62988. The structure at item 13 represents the opposite side of the reaction coordinate curve. We can improve upon this calculation by changing the step size of the IRC run, and/or by increasing the number of steps calculated at runtime. Needless to say, both options increase computational time! The results of this run are shown on the graph below:

For this particular run, I have an activation energy of 0.02886 hartrees in one direction and 0.03211 hartrees in the other. These are relatively close, as the graph also suggests. Values closer to experimental could be reached with the use of better basis sets, but these are sufficient to give us a sense of the behavior of this particular reaction.

Developed by
Graphic of Shodor Logo