Creating Gaussian 94 Input Files

Gaussian94 requires very little user input. To submit a job to Gaussian94, the user creates a relatively simple input file. This file should have the extention ".inp". For example, a water file might be titled "water.inp".

The general format for Gaussian94 input files is as follows:

Line 1: Link0 section (not used in Lab 1, defines the location of scratch files)
Line 2: Route section -- specifies the type of job, approximations to be used
Line 3: Blank line
Line 4: Title section -- provides a title for archiving and reporting purposes
Line 5: Blank line
Line 6-?: Molecule specification -- gives the structure of the molecule to be studied
Line ?+1-??: Variables section -- listings of variables to be used in the input file
Line ??+1: Blank line

Notice the emphasis on the blank lines. They have to be there, and forgetting the blank lines, especially the one at the end of the file, is the foremost reason why beginning users of Gaussian94 don't get successful runs!

This reading explores in more depth each of the sections above.

Link0 section

The Link0 section has the purpose of establishing scratch files to be used in the computation. The most common scratch file is the "checkpoint" file. The checkpoint file serves to store useful intermediate datasets, such as structures, wavefunctions, and force constants. Generally, the checkpoint files are useful only to the program, not to you as output files to be evaluated. There are, however, several utility programs, such as "formchk", which can be used to format the checkpoint files for analysis by human eyes or visualization software. A checkpoint file can be requested by the use of this command in the Link0 sections:

%Chk=filename

We will probably not make use of this option, in which case, that section can be left out entirely.

Route section

This section controls the computation by selecting the type of approximation and basis set to be used. The route section is specfied by the "#" character, and is followed by a blank line. The route section consists of a wide variety of keywords and options for controlling the computation.

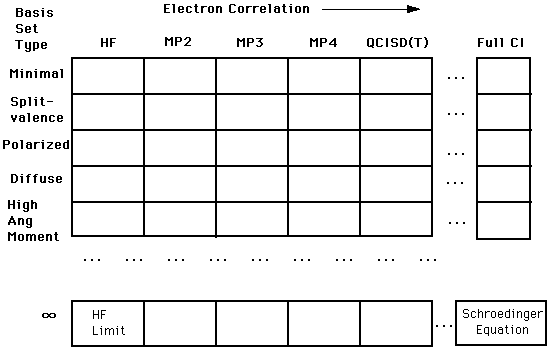
Approximation method: the approximation method is known as the "model chemistry". For the simple problems in this session, we'll use the Hartree-Fock approximation. You should recall that this method is the simplest and least accurate method, in that it does not take into account electron-electron correlations. It is, however, a good method for getting some insight into the properties of a structure. There are two "versions" of the Hartree-Fock model chemistry: restricted and unrestricted. The restricted method (RHF) is used for those molecules that have only paired electrons. Unrestricted Hartree-Fock (UHF) is to be used for those structures that have lone electrons in the structure. The Hartree-Fock model chemistry is the theory that will be the most useful for our purposes. Other model chemistries with a brief description are:

Configuration Interaction (CI): briefly, full CI methods represent a mixing of all possible electronic conditions of the structure. CI represents a highly rigorous computational technique.

Möller-Plesset Perturbation Theory (MPx, where x is a version number): builds on the Hartree-Fock model chemistry by including some higher electronic approximations.

Your choice of model chemistry is specified in the Route section, such as:

# RHF
# CIS
# MP2

Basis set: your choice of basis set is also specified in the Route section, separated from the model chemistry by a "/". Basis sets represent a starting "guess" on the mathematical "shape" of the wavefunction. Remember that the basis set represents a "kick-start" to the mathematical engine in Gaussian94. The combination of model chemistry and basis set dictates the complexity and accuracy of the solutions obtained. Keep in mind that the "goal" is to get closer and closer to a solution of the Schroedinger equation:

The finalized route section might look like these:

# RHF / STO-3G
# HF / 6-13G OPT
# HF / 6-31G* SCF=DIRECT FREQ GUESS=READ GEOM=CHECK

In the first example, we are asking for a restricted Hartree-Fock approximation using the basis set STO-3G (Slater-type orbitals, 3 gaussians). In the second example, we are requesting the Hartree-Fock approximation with the 6-31G basis set, and we want Gaussian94 to optimize the geometry. In the third example, we are using Hartree-Fock, with 6h 6-31G polarized basis set. We want it to do a direct self-consistent field calculation, with a frequency calculation being performed, with the initial guess coming from a checkpoint file, and the initial geometry also coming from the checkpoint file.

Title section

The title section is just a label for you to use in keeping track of your output. The title is placed on a single line by itself, without any special characters preceeding it.

Molecule specification

This section is used to describe the basic beginning characteristics of the molecule to be studied: charge, spin multiplicity, units, and coordinates of the molecule.

Charge: a positive or negative integer indicating the total charge on the molecule. For example, the charge on water is 0; the charge on ammonia (NH3+) is 1.

Spin multiplicity, or multiplicity for short, is the same as the multiplicity that MacSpartan uses in its calculations. For our purposes, we are only concerned with multiplicities of 1 or 2. Molecules with all electrons in pairs have multiplicity of 1, while molecules with a single unpaired electron have multiplicity 2.

Now comes the fun part! We must provide a starting geometry of the molecule of interest. You have three options on how you might do this:

Redundant internal coordinates: this is the "default" or preferred method for Gaussian94, but we're not going to use it. Gaussian converts the coordinates given to redundant internal coordinates for some calculations anyway, without your ever seeing it.

Cartesian coordinates: the basic geometry of the molecule can be specified by a simple x-y-z coordinate system. These values can be determined a number of ways, including from experimental data or through the use of other computing tools or molecular editors. We can get Cartesian coordinates from a number of sources, including MacSpartan or some visualization tools. Below is an example for formaldehyde:

ATOM		X		Y		Z
C(1)		-0.227		0.204		0.079
O(2)		0.642		-0.584		-0.208
H(3)		-1.303		-0.062		-0.017
H(4)		0.019		1.227		0.442

These numbers are in units of Angstroms.

Other Cartesian coordinates will be provided if you want to do some exercises with G94. Ask a presenter for more help if you need other coordinates.

Internal coordinates, also known as a "Z-matrix". The Z-matrix input defines the molecule in a set of internal coordinates. A number of recent studies suggest that the Z-matrix is probably the worst of the three methods, not only in its construction but also it is ability to optimize cleanly. We will not focus much on Z-matrices beyond a basic explanation of their structure. They are useful in some examples, as you will see.
This method follows this algorithm:

1. Place the first atom at the origin
2. Place the second atom along the Z-axis using a bond length
3. Place the third atom in the XZ-plane using a valence angle (angle between three atoms) and a bond length.
4. Place the fourth and subsequent atoms by defining a dihedral angle with the plane of three other atoms, a valence angle and a bond length. A dihedral angle is the angle between four atoms. That is, the dihedral angle for atoms ABCD is the angle between the plane containing atoms ABC and the plane containing atoms BCD.

So, each line follows the format
Atomname atom1 bondlength atom2 angle atom3 dihedral
However, not all of these specifications may be needed for the first two or three atoms. Atomname is usually the element symbol followed by an integer, as you will see below. "atom1", etc, are the atom names of other atoms to which the geometry details refer.
Below is a Z-matrix for hydrogen perioxide.
```
O1					
O2	O1	1.404
H1	O1	0.942	O2	92.50
H2	O2	0.942	O1	92.500	H1	-180.00
```
In this Z-matrix, the leftmost oxygen is designated as O1 (the numbers are optional, but helpful). The second atom is oxygen O2, and has a bond length of 1.404 Angstroms from the first oxygen. The leftmost hydrogen is designated as H1; its relationship to O1 is with a bond length of 0.942 angstroms, with an H1-O1-O2 angle of 92.5 degrees. The second hydrogen, H2, has a bond length of 0.942 angstroms from O2, has a valence angle of 92.5 degrees for H2-O2-O1, and a dihedral angle (going counterclockwise) of -180 degrees for H2-O2-O1-H1.
Variables section
In this section, you can establish variables that replace numerical values in the Z-matrix. An example molecule specification for water is as follows:

0 1
O
H 1 r
H 1 r 2 a
Variables:
r 1.0
a 105.0

In this Z-matrix, the variable "r" represents the bond length, and the variable "a" represents the bond angle. One of the values of using a variables section is that it allows you to easily modify common values. It will also be used in performing geometry optimizations in later sessions.

Developed by
The Shodor Education Foundation, Inc.
Copyright © 1998
Last Modified:
Questions or comments about this page should be directed to gotwals@shodor.org