Case Studies and Project Ideas: Windkessel Cardio

Medicine and the Biosciences Main Page

Other Case Studies and Project Ideas

Cardiovascular Physiology: The Windkessel Model

Source:

Narrative and case study design by Robert R. Gotwals, Jr.

Goal:

To learn about basic cardiovascular physiology through the building of a simplified three-compartment simulation model.

Background Reading:

Three Windkessel compartments--representing the arteries, veins, and right atrium--have been interconnected to complete the circulatory loop. Each compartment is characterized by two variables, pressure and volume, and two parameters, compliance and unstressed volume. Total blood volume is assumed to be 5000 ml.

In the equations that follow, P, F, and V represent pressure (mmHg), flow (ml/min), and volume (ml), respectively. C is compliance (ml mm/Hg), Vo is unstressed volume (ml), and R is resistance (mmHg min/ml).

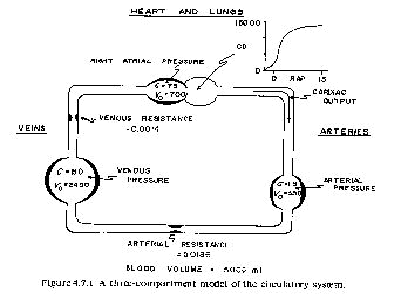
Flow through a blood vessel is determined by two factors: 1) the pressure difference between the two ends of the vessel, called "pressure gradient," which is the force that pushes the blood through the vessel, and 2) the impediment to blood flow through the vessel, which is called vascular resistance.

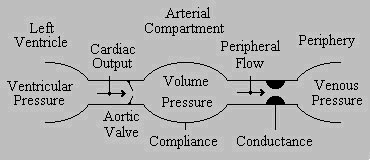
This Windkessel model consists of four components:

Left Ventricle
Aortic Valve
Arterial Vascular Compartment
Peripheral Flow Pathway

The independent variable is time (t). The units are minutes.

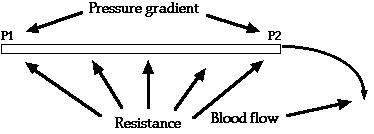
P1 represents the pressure at the origin of the vessel; at the other end the pressure is P2. Resistance to flow occurs as a result of friction all along the inside of the vessel. The flow through the vessel can be calculated by the following formula, which is called Ohm's law:

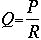
Q is blood flow

P is the pressure difference (P1-P2) between the two ends of the vessel

R is the resistance

This formula states that the blood flow is directly proportional to the pressure difference but inversely proportional to the resistance. That means that the pressure of both ends of the vessel are different and that determines the rate of flow. For instance, if the both ends of the segment were 100 mm-Hg pressure and yet no difference existed between the two ends, there would be no flow despite the presence of 100 mm-Hg pressure.

Building the Model:

The algorithm for this model is as follows:

Initial values for this model:

Arterial volume = 1000 mL
Right atrial volume = 1000 mL
Venous volume = 3000 mL
Arterial compliance = 1.5 mL mm-Hg
Arterial resistance = 0.0186
Intrapleural pressure = 4 mm-Hg
Right atrial compliance = 75 mm-Hg
Unstressed arterial volume = 350 mL
Unstressed right atrial volume = 700 mL
Unstressed venous volume = 2450 mL
Venous compliance = 150 mm-Hg
Venous resistance = 0.0014

You should run this model for 1 minute, using very small step sizes (0.01 is recommended). You should also use RK4 integrator. We are fundamentally interested in the amount of cardiac output coming out of the arteries.

Using the Model:

Once the model is constructed, your task is to determine the sensitivity of the model to various changes in parameters. Suppose, for example, that you have a decrease in the vascular resistance in the amounts of 25%, 50%, and 75%? What is the effect of these changes on cardiac output? Which parameter has the most significant impact on cardiac output? You might want to use a spreadsheet to help.

Developed by
Graphic of Shodor Logo