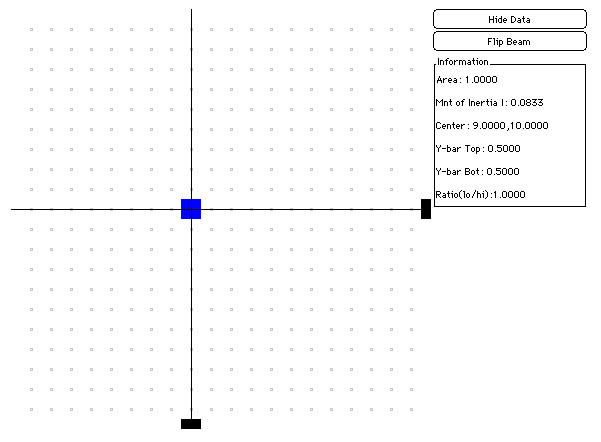
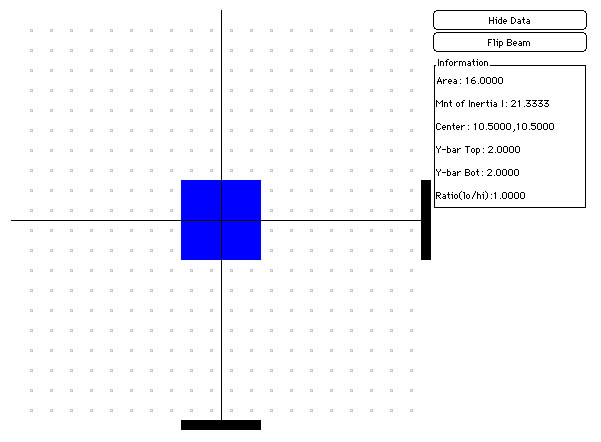
So what do the black lines in the computer model represent? For a single blue square or a rectangular area, each line divides the block in two equal parts, and the lines cross in the 'middle' of the area (you may need to build your own examples in the applet to see better!):
|
|
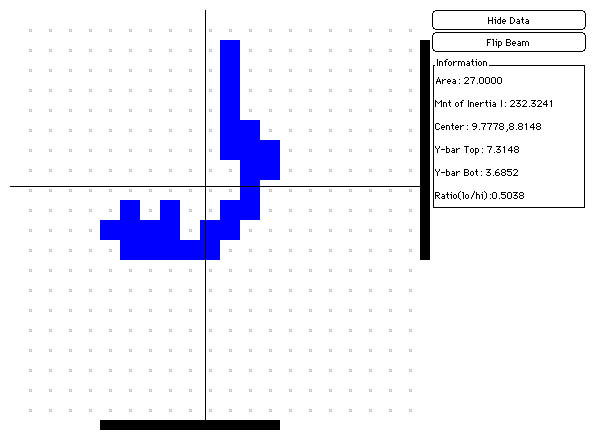
We build more complicated shapes out of small square areas. Each square is located in a particular position (column X and row Y), and the black lines represent the average position of each of these squares. For example, in the grid below, there are two squares in column 8, one in column 9 and one in column 10, for a sum of 8+8+9+10=35 and an average of 35/4 = 8.75 . We also see that there are three squares in row 6 and one in row 7, for a sum of 6+6+6+7=25 and an average of 25/4 = 6.25 . Notice that the data table reads 'Center = 8.75,6.25'.
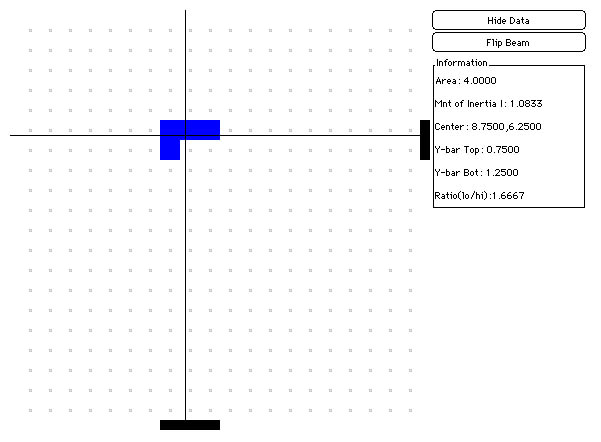
The point where the black lines cross is the average position of the square areas that make up the shape. This point is called the center of area or the centroid. When we build the same shape out of Legos, each Lego unit has (nearly) the same mass, so the center point can then be called a center of mass. Because we are looking at the behaviour of our structures due to gravity, the center of mass can also be called the center of gravity.
Note: The centroid and the center of gravity are the same in this case because each Lego unit is made out of similar materials, and thus each area has the same mass. If we had some Lego units made out of something heavier (a metal of some sort, perhaps), or if we used Legos that were two units thick, they would contribute the same area, but more mass. A double-thick Lego would need to have it's position counted twice in the average for center of mass (and center of gravity), but only once in the average for center of area, and we would get different results for the centers. As long as we use single-thick Legos, however, our computational model that shows the centroid will also represent the physical center of gravity.
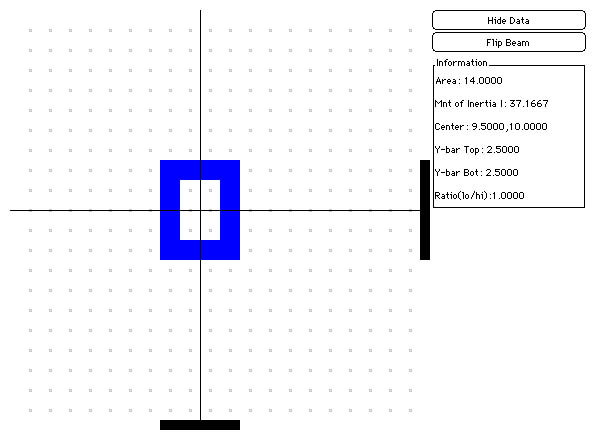
For certain shapes, a centroid may actually look like it is outside the shape! Shapes with holes in them and concave shapes (shapes with identations - think caves) will often have a centroid that is not inside the shape itself!
|
|
So here is the final question. How does the center of gravity relate to whether a structure will STAND or TOPPLE? Use the computer model to test some of the physical systems you have recorded. Where are the black lines for structures that STAND? Where are they for structures that TOPPLE?
| On to page 8! |
 The Shodor Education Foundation, Inc.
The Shodor Education Foundation, Inc.