
Mathematical Models in ScienceAuthentic Science
Matching Algorithm, Application and ArchitectureModern, scientifically valid models must be built on a firm foundation drawing from computation, theory, and experiment. Confidence in the computational aspects of such models is built from proper matching of the computer algorithm and architecture to the application.  The Progression from Qualitative to Quantitative ModelsThe learning curve for numerical modeling, as pictured here, may start with a qualitative "hand-waving" model -- for which the visualization is the model-- where simple theory and experimental data give rough insight into behavior. This insight may be refined by formulating the theory as mathematical models and then solving these models with a range of increasingly sophisticated tools, matching the tools to the complexity of the problem. The progression to more quantitative models begins with running other people's models, then modifying these models, and ultimately creating new models, tuning the numerical solutions and visualizations along the way. 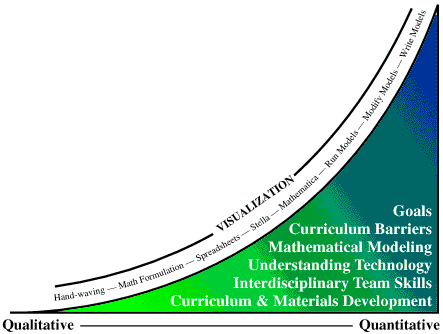
Bob Panoff's Vistas Talk
Last Update: June 6, 1998 Please direct questions and comments about this page to WebMaster@shodor.org © Copyright 1998 The Shodor Education Foundation, Inc. |