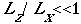
Meteorological fields are governed by a set of nonlinear partial differential equations. These equations represent the conservation of momentum (wind velocity), thermodynamic energy, mass of air, pressure, and water. The equations can be expressed in a x, y, o framework where x and y are the horizontal coordinates and o is a terrain-following vertical coordinate . The hydrostatic and incompressible assumptions are usually considered valid for the airflows of interest within the SJVAQS/AUSPEX study region. The hydrostatic assumption is appropriate when the ratio of the vertical to the horizontal scale of the circulation is substantially less than unity:
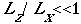
This requirement is discussed by Pielke (1984). The hydrostatic assumption may not be valid over complete e terrain with extreme variations in terrain. Approximate incompressibility is satisfied if the ratio of the vertical scale of circulation to the scale height of the atmosphere is much less than unity :
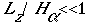
where H(alpha) is the atmosphere-scale depth defined as RdTo/g (Rd is the dry air gas constant, To is a reference temperature, and g is the gravitational acceleration). Assuming To =273.15 K results in H(alpha) =8002 m, this equation holds for an Lz of several hundred meters. Another criterion for incompressibility is that the density variations represent a small fraction of the basic- state density. The pressure and temperature fluctuations in the phenomena to which this model is potentially applicable are at most a few tens of millibars and tens of degrees, so the density fluctuations are correspondingly small.
The terrain -following vertical coordinate z* is defined as:

The governing equations in the terrain-following coordinate are then expressed as:
u-momentum
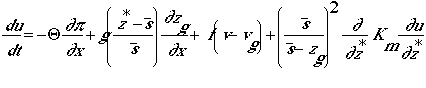
v-momentum
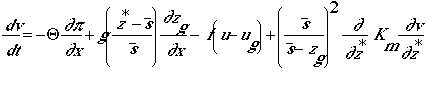
w-momentum (simplified equation to obtain the hydrostatic approximation)
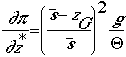
thermodynamic
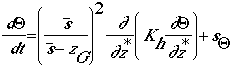
conservation of moisture energy
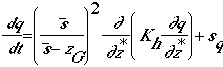
continuity equation
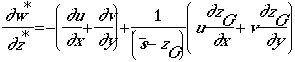
In these equations

A detailed discussion of these equations is provided by Pielke (1984). Other coordinate systems can also be used. For example, an x, y, z coordinate system is used in the San Jose model, and an x,y, (sigma)p coordinate is used in the MASS, SUNY version of NCAR/PSU,and ERT/CMC/PBL models. The x,y, (sigma)z coordinate system is used in the Drexel , CSU, RAMS, and Los Alamos models. These models are by Pielke (1994).
The initial and boundary conditions that are associated with the basic equations are essential components of the meteorological model. Initial conditions are needed for wind velocity, temperature, pressure, and water. Generally , data are not available on a spatial resolution sufficiently fine for the modelŐs grid resolution. Using objective techniques, interpolation n from available data can be used to develop an initial field consistent with the modelŐs spatial resolution. The initialization of the meteorological model may require integration of the model equations over a period of time so that the model can adjust to initial conditions.
Boundary conditions include lateral , top, and surface conditions. Lateral boundary conditions can be provided from National Weather Service synoptic data with proper spatial and temporal interpolation. The top boundary conditions must be set up carefully to avoid downward reflection of wave energy, which would be artifact of the limited vertical extent of the model domain. The surface boundary conditions must reflect the exchange of heat, moisture, and momentum between n the ground and the lower layer of the atmosphere.
In addition to the basic equations, some parameterizations need to be included in a meteorological model to take into account physical processes that are not necessarily treated by the basic equations. Such processes may include:
The meteorological model must have several basic characteristics to resolve the atmospheric dynamic and thermal features relevant to transport and dispersion in the SJVAQS/AUSPEX domain. These characteristics include:
Data assimilation techniques can also improve the performance of meteorological models, although difficulties such as unstable solutions may occur. The partial differential equations that govern the behavior of the meteorological variables are modified with the addition of terms that nudge model predictions toward measurements. Model results can also be combined with observational information through objective analysis techniques(Kessler and Douglas 1989).
Several numerical techniques may be used to solve the primitive equations. Major attributes of the numerical techniques include the ability to conserve mass and energy and to represent the phase speeds and amplitude of propagating atmospheric features to address these characters.
An emissions model uses emissions data and related information available in the emissions database archived by the California Air Resources Board (ARB). The ARB uses these data bases to publish annual emissions inventories. However, the emission estimates reported in the annual inventory are in fact derived from emission models. Emission estimates are made combining emission factors and activity data. The emission factors and activity data are often derived from averages of test measurements and proration of national or statewide statistics. The ARBŐs emissions model results can be extended by 1) combining them with additional information such as nontraditional source categories (e.g., biogenics) or non criteria pollutants (e.g., NH3); 2) spatially disaggregating area source emissions to modeling grid cells; 3) temporally allocating the emissions; and 4) chemically speciating and classifying by size all emissions in the region for use in the air quality model. The emissions model must account for all relevant emissions source categories from anthropogenic and natural sources.
The emissions model comprises numerous submodels or mode l components for estimating emissions for each source category, and for spatially disaggregating , temporally allocating, chemically speciating, and size-classifying emitted pollutants (Dickson et.al. 1994). The submodels must account for emissions of total organic gas (TOG), NOx, CO, sulfur oxides(SOx) particulate matter, and NH3. NOx and the reactive portion of TOG (reactive organic gas) are precursors to the formation of ozone in the atmosphere; CO emissions, to a lesser degree, also play a role on the formation of ozone. Particular matter emissions affect visibility, and SOx emissions contribute to visibility impairment and acid deposition.
Point source emission estimates rely on facility-specific information such as operating schedules and actual throughput data, whereas area source emission models are based countywide or statewide activity levels and typical usage patterns. On-road motor vehicle emissions are calculated by a series of emissions models developed and operated by the ARB and the California Department of Transportation. In general, the models used to calculate on-road motor vehicle emissions are the most complex. Typical approaches for estimating on-road motor vehicle emissions include:
The emissions model develops emission estimates by:
All activity data and emission factors are assembled into a regulatory reference data base designed for incorporation of updates from local agencies. From this data base, estimated emissions are generated by regulator y emissions model. These emission estimates are based on activity levels and emission factors for stationary area sources, major point sources, and motor vehicles. The resulting regulatory emissions data base which includes all the criteria pollutants (CO, NOx, total hydrocarbon, and particulate matter ) acts as a clearinghouse, whose function is to provide a central point to process emissions data into a consistent system from which region- and model-specific sub inventories can be extracted. In addition, as the result of special studies, the regulatory emissions data base may contain NH3 emissions and criteria pollutant missions from natural sources. Uncertainty and variability analysis are performed to quantify the reliability of the estimated emissions.
The modeling emissions inventory , referral to as a model emissions field , requires a submodel that processes the appropriate emissions from the emissions data base into the necessary model-ready format. The modular design of the emission preprocessor system submodel provides maximum upgrade capabilities and allows the addition of new data and techniques. The model preprocessor allows variable definition of the modeling domain, assignment of temporal profiles by source category, and spatial allocation of emissions by specified location of disaggregation surrogates. Further processing of the emissions is needed to determine the speciation of VOC into the chemical for total hydrocarbons are generated by a separate module to facilitate new data as they become available. the final result of the emission preprocessor system submodel is an emissions field in model-ready format. Typically, this is an hourly, gridded field for all model input emission species. Chinkin et al. (1990) provide a detailed discussion of the complete emissions model, and a detailed summary is given by Dickson et al.(1994).
Emissions models have not been subject to comprehensive evaluations, and large uncertainties remain for many components (e.g., speciated hydrocarbon emissions, size and distribution of particulate emissions, fugitive dust emissions, and biogenic and geogenic emissions). When fully implemented, overall emission uncertainty estimates generated in each of the component uncertainty modules should accompany the final emission estimates reduction requirements.

Molecular diffusion is neglected, because it is small compared to turbulent diffusion. The diffusivity tensor is generally approximated by three terms, and he cross-directional diffusion terms are neglected. Assuming that the atmosphere is an incomprehensible leads to Vv=O, the atmospheric diffusion equation then simplifies to the following equation:
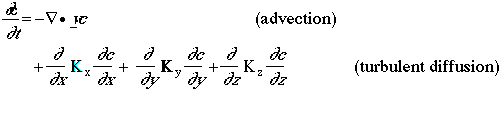
where Kx and Ky are the horizontal diffusion coefficients, which are generally identical in Eulerian models, and Kz is the vertical diffusion coefficient. In addition to treatment of transport and diffusion within the three- dimensional grid mesh, it may be appropriate to treat subgrid-scale dispersion of plumes emitted from major point or line sources. The atmospheric diffusion equation also applies to these subgrid-scale phenomena; however, there are several difference in the implementation of the atmospheric diffusion equation to a mesoscale and to local-scale (i.e., subgrid-scale) phenomena. For example, the values of the turbulent diffusion coefficients are different since they represent the near-source diffusion of pollutant rather than the background diffusion represented in the grid mesh.
It is not possible to obtain an analytical solution the atmospheric diffusion equation except for simple, specific functions of the wind field and diffusion coefficients. For most practical applications at the mesoscale, the solution of the advection and diffusion terms requires different numerical techniques. The advection term is the most difficult to solve because of its hyperbolic nature. Numerical solution of a partial differential equation will lead to numerical diffusion, and it is essential to limit the extent of this numerical diffusion to obtain an accurate solution of pollutant transport. There are several numerical techniques that attempt to limit numerical diffusion. Finite element techniques (e.g., the Sulfur Transport Eulerian Model [STEM], techniques based on cubic spline functions (e.g., the Acid Deposition and Oxidant Model [ADOM], and techniques based finite differences (e.g., the Regional Acid Deposition Model [RADM] have been used t simulate pollutant transport. Finite element and cubic spline techniques are the most appropriate to avoid numerical diffusion but may result in negative solutions, which need to be controlled to maintain mass conservation. Therefore, all numerical techniques have their merits and shortcomings, and there is currently no consensus on which techniques should be favored. Seigneur (1994) gives an overview of the numerical techniques used in several-dimensional air quality models. The solution of the diffusion terms can be handled by standard finite difference techniques , and generally does not result in significant numerical difficulties.
Transport models can be evaluated against analytical solutions of the advection equation to assess the extent of numerical diffusion. The full diffusion equation (i.e., transport and diffusion) can be evaluated against tracer data . However, limited evaluation has been performed.
The equations used to calculate the major characteristics of clouds and fog typically involve an energy balance equation and mass continuity equations for water in its different phases (vapor, cloud droplets, raindrops, and ice crystals). The mass continuity equations are based on parameterizations of water microphysics and may differ to the model used.
Examples of cloud physics models include those of Walcek and Taylor (1986), Hales (1989), Nair and Peters (1989), Seigneur and Wegrecki (1990), and Karamchandni and Venka tram(1992). Because no normal performance evaluation of these models has been conducted, it is not possible to recommend a specific model. Treatment of advection fog is similar to that of stratus clouds. The work of Pandis and Seinfield (1989a) is a good reference for the treatment of radiation fog.
The energy and mass continuity equations are solved with standard numerical techniques such as finite difference techniques. There are no major difficulties in the solution of these equations. However, one must be cautious to control the integration time steps to avid negative concentrations in the water budget equations. Negative concentrations may occur during the calculations of phase changes for water or transport through the gridded domain. Precipitation rates calculated by meteorological models have been compared with data. No detailed evaluation of cloud microphysics has been performed.

The ordinary differential equations that govern gas-phase chemical kinetics are numerically stiff (i.e., the typical half-lives of the chemical species cover a wide range of values). Using time steps commensurate with the half-life of the fast reacting species would result in prohibitive computational expenses. One possibility is t assume pseudo steady-state for fast-reacting species, thereby removing the numerical stiffness. This approach requires the numerical solution of a nonlinear set of algebraic equations. The other possibility is to use a numerical technique suitable for stiff systems. However, this approach is computationally more demanding than the former approach and is rarely used in three-dimensional air quality models. Therefore, the use of steady-state approximations is recommended for the solution of gas-phase chemical kinetic equations.
The chemical kinetic equations that govern the change in concentrations of chemical species are derived the mechanism that is assumed to represent atmospheric chemistry. These gas-phase mechanisms describe the of NOx, organic compounds (e.g., hydrocarbons), and SO2. Such mechanisms may include several thousand reaction. However, computational constraints require that a more limited number of reactions be included in a chemical mechanism. Therefore, chemical mechanisms have been developed using assumptions reactions are included and the condensation process pertains solely to the organic chemistry . The three major mechanisms that are currently in use in air quality models are:
These mechanism differ in their approach to condensing organic chemistry, but have similar treatment of inorganic chemistry. The mechanisms offer similar performances when compared to experimental data obtained in smog chambers (Dodge 1989). Therefore, each mechanism represents the present state of knowledge of atmospheric chemistry and is therefore suitable for the treatment of gas-phase chemistry. The performance of these mechanisms has not been tested for low concentration levels. There are also uncertainties about the kinetic and mechanistic details of gas-phase chemistry. Such uncertainties include the chemistry of long-chain alkanes; the products of the reaction of alkanes with OH, NO3, and ozone; the photolysis rates and quantum yields of aldehydes; the chemistry of aromatics, NHO3, and HONO; and the formation of condensable organics.
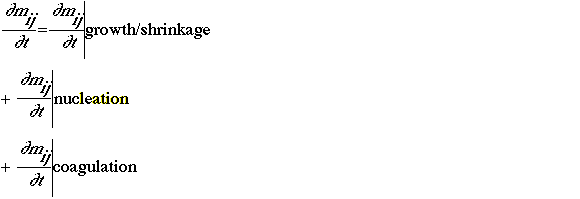
where mij is the mass of species j in the size range I. It is assumed that, diffusion, emission, and removal of aerosols are treated in the transport and diffusion component, emissions model, and deposition components. The growth-shrinkage term results from the condensation or evaporation of chemical species on the aerosol surface. Consideration may occur as a result of the formation condensable species in the gas phase, changes in equilibrium conditions, reaction of a chemical species on the aerosol surface, or reaction of a chemical species in the aerosol-liquid phase. Evaporation may occur as a result of the formation of a volatile species in the aerosol or changes in equilibrium conditions.
The mathematical representation of these processes varies Nucleation is an important process in polluted areas, and its treatment is important only in areas where background aerosols levels are low. The mathematical representation of this process can be treated either as a source term for nucleating aerosols (e.g., Pilinis et al. 1987) or as a source term for the lower range of the aerosol size distribution (e.g., Hudischewskyj and Seigneur 1989). The coagulation process is well simulated by the standard coagulation equations of Fuchs, and the condensation/ evaporation processes are well simulated by diffusion equations (e.g., Friedlander 1979). All models are based on the same general dynamic equation and differ only in the numerical approximations to this equation. In addition to the dynamic equation, it is necessary to simulate the thermodynamics of the aerosol system. The thermodynamic model consists of equilibria between several species (e.g., sulfate, nitrate, ammonium, and water) in several phases (gas, liquid, and solid). The mathematical model is a set of nonlinear algebraic equations. The assumption step may then to be considered.
Saxena et al. (1986) have applied three thermodynamic models (KEQUIL, EQUIL, and MARS) of inorganic aerosols to realistic cases and have compared the computational requirements and accuracy of these models. The models simulate the thermodynamics of a sulfate/nitrite/ ammonium/water system. The KEQUIL Model provides a comprehensive treatment of the thermodynamics of the system and includes the effect of aerosol size on the gas/aerosol equilibrium (i.e. the Kelvin effect). The EQUIL Model uses the same thermodynamics as the KEQUIL Model, but does not take the Kelvin effect into account. MARS uses a simplified treatment of aerosol thermodynamics by discarding minor thermodynamic equilibria and also does not take the Kelvin effect into account. All three models simulate the chemical composition of a sulfate/nitrate/ammonium/water aerosol within an average of 7% uncertainty. The EQUIL Model is seven times more computationally efficient than the KEQUIL Model; MARS is 50 times more computationally efficient than the EQUIL Model. Pilinis and Seinfeld (1987) developed the SEQUILIB Model, which uses a simplified treatment of aerosol thermodynamics. It does not treat the Kelvin effect, but takes into account chloride, sodium, sulfate, nitrate, ammonium, and water. For a sulfate/nitrate/ammonium/water aerosol, the SEQUILIB Model has an accuracy similar to that of the EQUIL Model and MARS, and has a computational efficiency between that of the EQUIL Model and MARS (Seigneur 1990).
MARS is valuable when a large number of aerosol calculations must be carried out. Upgraded to include treatment of chloride and carbonate (these species are important because they may react with nitric acid to form coarse nitrate aerosols), MARS may be the most appropriate choice to simulate inorganic aerosol chemistry.
Organic aerosol chemistry is still a topic of research because of the complexity of the chemical mechanisms that lead to the formation of condensable organic species and the difficulty of characterizing their thermodynamic properties. We recommend that a scientifically sound and computationally efficient mechanism for organic aerosol formation be used in the PM-10 model. The work of Grosjean and Seinfeld (1989) should provide the basis for developing such a model. This work, which presents a parameterization of the formation potential of secondary organic aerosols, needs to be expanded further. Specifically, the parameterized coefficients for organic aerosol formation should take into account the ambient concentration levels of hydroxyl radicals (OH) and ozone, and should also include nighttime oxidation mechanisms of organic compounds by nitrate radicals (NO3. The parameterization should then be cast in a format that is compatible with the formulations of standard chemical kinetic mechanisms such as the CBM-IV, the Carter-Atkinson-Lurmann-Lloyd mechanism, and the RADM mechanism.
Aerosol chemistry is generally limited to the aqueous oxidation of SO2 by a few chemical pathways (oxidation by hydrogen peroxide and by oxygen in the presence of iron and manganese). The aerosol chemistry model consists of chemical kinetic equations in the aqueous phase, aqueous ionic equilibria, gas/liquid equilibria, and calculation of aerosol pH. (the aerosol pH is calculated as part of the aerosol thermodynamic model). The model of Saxena and Seigneur (1987) provides a treatment of aerosol chemical kinetics.
Solution of the general dynamic equation involves growth/shrinkage, nucleation, and coagulation terms. The last two terms are solved by standard numerical techniques with good accuracy. Numerical difficulties arise with the solution of the growth/shrinkage term, because its hyperbolic nature leads to numerical diffusion and dispersion. Continuous, sectional, and log-normal representations of the general dynamic equation have been used based on the mathematical form of the aerosol-size distribution.
Seigneur et. al. (1986) have compared the computational requirements and accuracy of the representations. The continuous representation is the most accurate, but is large computational requirements limit its use for large-scale applications. The sectional representation is fairly accurate for the simulation of coagulation but can show significant numerical diffusion for the simulation of condensation. Its computational requirements depend on the number of sections (i.e. size ranges) considered but are typically less than those of the continuous representation. The sectional approach has been used in three-dimensional Eulerian grid models. The log-normal representation is the most computationally efficient approach. The uncertainties associated with the simulation of condensation are equal to or less than those of the sectional method. The simulation of coagulation for high aerosol concentrations (i.e. aerosol levels typical of polluted urban conditions) may lead to larger uncertainties than those of the sectional method. Based on the results of this comparison, it appears that the log-normal representation presents the best combination of computational efficiency and predictive accuracy.
The thermodynamic model consists of a set of nonlinear algebraic equations. A comprehensive system of thermodynamic equilibria between sulfate, nitrate, ammonium, and water requires iterative numerical techniques (e.g., the KEQUIL and EQUIL models). Simplifications to the thermodynamics of the system can be made. These allow an easier solution of the system and, therefore, a reduction in computational costs (e.g., the SEQUILIB Model and MARS). Solution of aerosol chemical kinetics is generally straightforward, because few chemical reactions are involved, and there is no numerical stiffness.
Aerosol models have been evaluated with data collected in power plant and smelter plumes (Hudischewskyk and Seigneur 1989), and urban areas (Pilinis and Seinfeld 1988). Performance of aerosol models has been satisfactory. However, several uncertainties remain in the treatment of some aerosol processes (e.g. water content of the aerosol and secondary organic aerosols).

The nonlinear ordinary differential equations that govern aqueous-phase chemical kinetics are generally numerically stiff and, consequently, require the same numerical techniques as those used for the gas phase. The equilibrium relationship can form a set of nonlinear algebraic equations, although in most models the nonlinearity is limited to the calculation of pH. An iteration technique is therefore required to resolve these equations. If the nonlinearity extends to chemical concentrations other than the hydrogen concentrations (for example, if a detailed treatment of the metals chemistry is considered), the iteration needs to be extended to several species to interactively solve the equilibrium equations (Morel and Morgan 1972).
Many chemical reactions occur in the aqueous phase. Consequently, chemical mechanisms can involve hundreds of reactions. Computational requirements of air quality models limit the use of such mechanisms, and more condensed aqueous-chemical mechanisms are generally used. Although the same basic chemical reactions are present in all mechanisms for droplet chemistry, there are differences in the treatment of radicals, metals, and organics. Recent aqueous-phase chemical kinetic mechanisms include those of Jacob (1986), Seigneur and Wegrecki (1990), Pandis and Seinfeld (1986b), and Nair and Peters (1989). Seigneur (1991) reviewed these models; a model that includes about 40-70 aqueous reactions is recommended.
The treatment of mass transfer from the bulk-gas phase to the droplets includes three steps: gas-phase diffusion, gas-liquid mass transfer, and liquid-phase diffusions. The simplest models assume that diffusion in the gas phase and liquid phase occurs rapidly, and that gas-liquid mass transfer (governed by Henry's Law) limits the rate of mass transfer between the two phases. Schwartz (1986) reviews the conditions under which diffusion can be neglected and concludes that in most cases gas-liquid transfer is governed by Henry's Law. However, in some cases, such as large drops (e.g., rain drops) or fast-reacting species (e.g., radicals), the diffusion steps become rate-limiting and must be included in a comprehensive model of the gas-liquid mass transfer.
No formal evaluation of aqueous-phase chemical mechanisms has been conducted. Cloud chamber experiments do not allow one to develop a data base for model evaluation as smog chamber experiments do for gas-phase mechanisms, because chemical sampling tends to disrupt cloud stability. Atmospheric data on cloud and fog chemistry have been collected, but transport processes contribute significantly to changes in cloud and fog chemical composition, and prevent the evaluation of aqueous-phase chemical mechanisms (.e.g., Seigneur and Wegrecki 1990). There is a need for collecting atmospheric data that would allow one to evaluate the performance of aqueous-phase chemical mechanisms. These data must provide sufficient information on transport processes.

The deposition velocity is generally calculated as the inverse of several resistances to transport. Transport steps usually considered for gaseous pollutants include:
For each of these transport steps, a resistance is calculated. The dry deposition velocity is then calculated as:
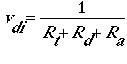
For gaseous pollutants, solubility and chemical reactivity are the major factors affecting surface resistance and net deposition velocity. For aerosols, downward transport toward the surface occurs by turbulent diffusion and gravitational settling. If all aerosols are assumed to remain on the ground, the deposition velocity can be calculated as three resistances acting in series (Rt, Rd, and RtRdvg) and one acting in parallel (vg) as follows:
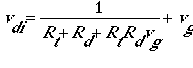
The third resistance in series (RtRdvg) is a virtual resistance, because it is a mathematical artifact of the equation manipulation rather than a physically relevant resistance. The dry deposition of aerosols depends on their size and mass. In addition, resuspension of particles into the atmosphere (as aerosols) may be an important process that is treated as a component of the emissions model. Sedimentation must be considered as a vertical flux in all layers of the model, whereas dry deposition affects only the lowest layer of the model.
Dry deposition fluxes are difficult to estimate, because direct measurements of deposition tend to disrupt the natural surface, and indirect measurements (e.g., those based on concentration gradients) require sophisticated experimental settings. Consequently, no comprehensive evaluation of dry deposition models has been conducted. There is a need for evaluating the dry deposition component using a sophisticated experimental setting. As part of the SJVAQS/AUSPEX study, a field experiment was performed in 1991 to collect data for evaluation of the dry deposition module. Plans for this study were provided by Hubbe (1989, 1990a, 1990b) and Pederson (1991). The evaluation is currently being performed by Hubbe and Pederson (1994).

This is an advection equation, and numerical diffusion will occur if the wet deposition process occurs over several model layers. Therefore, appropriate numerical techniques must be used.
No diagnostic evaluation of wet deposition components has been performed. Predicted and measured chemical concentrations in precipitation have been compared as part of three-dimensional acid deposition model evaluations. However, such evaluations are operational and include the effects of other processes such as emissions, transport, and chemistry. There is a need for designing experiments that will allow for the diagnostic evaluation of wet deposition components for cloud precipitation, cloud impaction, and fog settling.