Continuity Equation and K-theory

The continuity equation is the basis of many Eulerian-based air quality models. Fundamentally, this equation is a mass balance or mass conservation equation. One way to visualize this equation is as follows. Imagine a cone that is wide at one end and narrow at the other end. As air enters the wider end of the cone, it has a specific speed. As the cone becomes narrower, the air speeds up. The flow rate, however, remains the same. Flow rate is defined as:

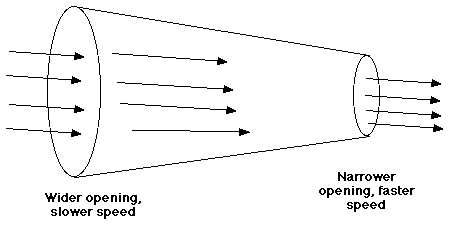
Flow rate = area x velocity

Since the flow rate is a constant at all points along the cone, we can define the continuity equation in these terms:

Area x velocity = a constant

 Graphic of wind cone

The equation at right shows a simple form of the continuity equation. You can investigate the behavior of this equation with the continuity equation calculator. This equation looks at the change in air density as a function of time with wind coming in three dimensions. In this case, what is being conserved is the mass of the air. None of the air molecules are being lost or changed by any other process. 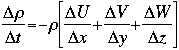Graphic of simple continuity equation

The continuity equation used in models such as CAMx look at the change in each species of pollutant over a period of time. Like the simpler algorithm above, the concentration of pollutant is being conserved. The physical model for horizontal advection diffusion is described as the "continuity equation closed by K-theory", which leads us to a discussion on K-theory. 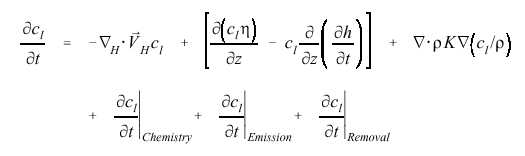Graphic of continuity equation for concentrations

K-theory

One of the problems with atmospheric equations (such as the continuity equation, the ideal gas law, the laws of thermodynamics, etc.) is that there are more unknown variables than equations, mostly due to the effects of turbulence. To be able to solve the mathematics, we need to have the same number of equations as we have unknowns. Any set of equations that has more unknowns than it has equations is called "open", and cannot be solved. We have what the mathematicians call a "closure problem". If we want the computer to solve these sets of equations, they need to be closed first. In meterorology, it is called "turbulence closure" since the problems are caused by the effects of turbulence.

A variety of different closure techniques are available, such as K-theory (described here) and the transilient turbulence theory (T3). Both of these methods are approximations to the effects of turbulence. The K-theory, so named becuase of its use of a parameter called the eddy viscosity or eddy diffusivity value (K, in units of m2-s-1), approximates transport of pollutants due to turbulence by only considering small eddies. The stronger the turbulence, the higher the value of K. Values of K can only be positive -- negative K values have no physical meaning.

One of the criticisms of K-theory as a closure approximation is that is does not work very well in an unstable planetary boundary layer (PBL), where values of K may be undefined.