Smog Photochemistry Modeling: A Case Study

Source: Model design by Dr. Kurt Peterson, Department of Environmental Engineering, Michigan Technological University. Used by permission. Narrative and case study design by Robert R. Gotwals, Jr.

GOAL

The goal of this case study is to learn about tropospheric photochemistry through modeling of a simple tropospheric chemistry causal loop system.

The case study uses the conceptual framework of computational science -- application, algorithm, and architecture. You should recall that application refers to the scientific problem of interest and the components of that problem that we wish to study and/or include. The algorithm refers to the numerical/mathematical representation of that problem, including any numerical method or recipe used to solve the algorithm. Finally, the architecture refers to the computing platform and software tool(s) used to compute a solution set for the algorithm(s) developed.

Application: Smog photochemistry in the troposphere

As you have read, Photochemical smog results from light, NOx, and VOC, and is composesd of ozone, NOx, and Peroxyacyl Nitrate and other VOC. It causes a number of health effects, such as breathing difficulties, aggrevation of respiratory illness, and possibly suppressed immune function. The following describes how to go about building a model which shows the relationship between NOx, VOC (in this case Carbon Monoxide), and Ozone.

The following is a look at the formation of photochemical smog from a kinetic perspective. Many of these equations should look familiar to you from previous lessons, but here is an opportunity to think about them as they all fit together! This chart shows the nine key equations of smog production, and the rate constant that affects the speed (or rate) at which the reaction takes place:

In this graphic, we see the involvement of the NOx system and the production of ozone. Basically, the ideas to remember are that the development of photochemical smog is dependent upon solar radiation, source emissions of hydrocarbons and nitrogen oxides, and atmospheric stability (for enhanced concentrations). Early in the morning, commuter traffic releases NO and hydrocarbons. At the same time, NO2 may decrease through because the sunlight can break it down to NO and O. The O is then free to react with O2 to form O3. Shortly thereafter, oxidized hydrocarbons react with NO to increase NO2 by midmorning. This reaction causes NO to decrease and O3 to build up, producing a midday peak in O3 and minimum in NO. As the smog ripens, visibility may be reduced due to light scattering by aerosols. Primarily due to the dependence on commuter traffic between surburbs and cities, there are presently more than 40 urban areas in violation of the US ambient air quality standard for ozone.

Algorithm Development

We can look at the change in concentrations of NO, NO2, and CO over time with this system of first-ordered differential equations. In the schematic below, we show the reactions by number from the graphic above. For example, R1 represents the photochemical reaction in which light energy hits a molecule of NO2 to form NO and singlet oxygen:

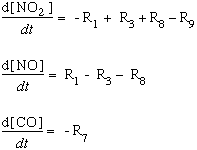
In the equations below, we substitute the kinetic components for each of the values of R:

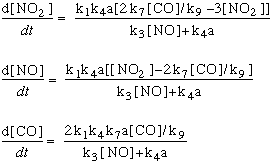
In these equations, the term "k" refers to the rate constants, and are numbered following the reaction numbers in the graphic above.

We wish to develop an algorithm to evaluate the photooxidation of CO in the presence of NOx. Equations can be derived for [NO2], [NO], and [CO], where the brackets [ ] mean the concentration of the species. Once developed, we need to integrate these equations numerically for the following sets of conditons and plot [NO2], [NO], [CO], and [O3] in parts per billion (ppb) as a function of time from t=00 to t=180 minutes with a time step around 0.1 min for a stable solution. Integration of these differential equations requires the use of some numerical method, such as Euler's method or one of several Runge-Kutta numerical methods, such as Runge-Kutta 2 or 4. As in all models, we start with some initial conditions and parameters. For this model, we will assume a temperature T of 298 degrees Kelvin (0 degrees Celsius is 273 degrees Kelvin, so 298 K is about 25 degrees Celsius, or about 80 degrees Farenheit, a nice warm day -- but you already knew how to do that conversion, didn't you!)

We can also look at the algorithms for this model broken down by input and output for each of the three species:

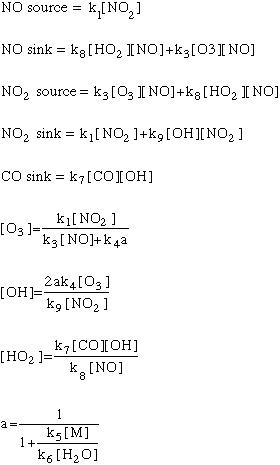
As in all models, we will need some initial conditions:

Initial Conditions (ppb)

SpeciesConcentration
[NO2]10
[NO]10
[CO]50

In each case assume that the photolysis rate constant for NO2 (R1 above) is:
kNO2 = 0.533 min-1

Some other helpful info to use:

[H2O] = 0.3x1018 [molecule/cm3]
[M] = 0.2x1020 [molecule/cm3]
k5=2.9x10-11 cm3/molecule-sec
k6=2.2x10-10 cm3/molecule-sec
Conversion factor: 1 molecule/cm3 = 4.08x10-11 parts per billion (ppb)
All of the other k values needed -- k4, k7, k8, and k9 -- can be found on the table of reactions.

***Keep in mind when you look at the online model, that values for initial [NO],[NO2], and [CO] are in molecules/cm3***

Architecture

In this case, the model was built using STELLA software, a program which uses differential equations to solve problems. After building the model on STELLA, it was converted into JAVA, a programming language. What you will see when you go to "run the model", is the JAVA version of this problem!

Last Update: