Relative Frequency Histograms

A graphical representation of frequency tables, which conveys the ideas of central tendency is a relative frequency histogram. Relative frequency histograms are constructed by grouping data into classes and calculating the number of data values that fall within each class. Bars (of equal width) are then drawn for each class with a height equal to the corresponding frequency. Look at the following example of a relative frequency histogram.  Notice, that by looking at the histogram we can easily locate the central trends.

1. Using our given data values, want to group them into classes of equal size.  For this example, we will use three classes. Time of Day [N2O] 0.05 m above surface ( nL / L ) 19:37 325 06:37 307 08:37 309 10:37 316 12:37 321 16:12 312

2. Now that we have grouped our data into a frequency table, we want to create a histogram which demonstrates our results.   Range ( nL / L ) Frequency of Measurements  in Range 300-310 2 311-320 3 321-330 1

3. After regrouping our data into a smaller number of categories, notice how the histogram does a good job of displaying the central tendencies of out data set.

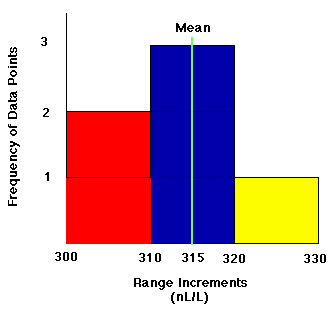Example of a Relative Frequency Histogram

If you would like more practice with histograms, there is a helpful activity located at www.shodor.org/interactivate/activities/histogram.