Traditionally, in physics we treat objects as being completely rigid when we study their motion. When dealing with the motion of the ocean or the atmosphere, clearly this is not so. It is also not possible to treat the ocean or the atmosphere on a particle by particle basis, however. Treating a single mole of gas is well beyond the capabilities of todays fastest computers. In fact, one of the most ambitious programming challenges to date in N-body problems is the study of the formation of structure in the universe. The largest N-body codes ever run, these codes track the individual motion and interaction of nearly 17,000,000 particles. However, if we were to consider the number of particles in a single mole of gas, we would need 6.0 * 1023 particles!
Fluid mechanics approximates the motion of uncountable numbers of atoms by looking at the bulk properties of a non-rigid mass, and tracking the change of density, bulk velocity, and pressure over time. In order to approximate the mean properties of a fluid (by fluid we mean anything which can flow freely and fill the volume it occupies), we assume three fundamental properties of physics.
Laminar flow
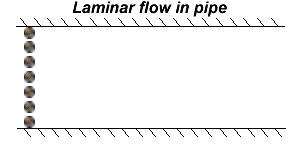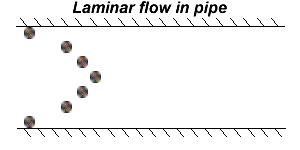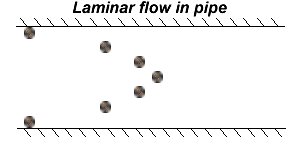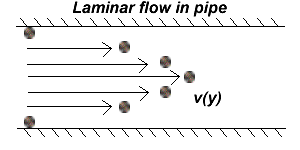
Steady flow with steady boundary conditions is referred to as laminar flow. One of the most common example of laminar flow is the steady flow of water through a pipe. The velocity of the water through the pipe is determined by the flox of water coming into the pipe, and the boundary condition that requires that the thin layer of water immediately next to the edge of the pipe must be stationary.

Turbulent flow
As teh speed of the water through the pipe increases, the shear between two adjacent streams of water can degenerate into turbulence. Turbulence refers to the growth of eddy currents and vortices due to the viscosity of a fluid.
Turbulence has no analytical solution, and studies of it generally center around determining what situations are favoarble for it. Even this is a difficult task, Heisendberg is reputed to have said of turbulence tht before he died he wanted someone to explain to him quantum mechanics, and after he dieed he wanted God to explain to him turbulence.
The following animation is of a forced fluid with a coriolis force. The simulations were designed by XXXXXX and can be found at YYYYYY. The image below is a typical state of a driven fluid with coriolis force, as might be found in Earth's atmosphere. Animations can be downloaded in QuickTime or MPEG format.

The Reynold's number of a fluid compares the bulk velocity through the macroscopic size scale of the fluid to the thermal velocity of fluid particles through the mean collisional path within the fluid. The Reynold's number is not a rigidly defined parameter, as it depends upon the size scale of interest. As a general rule, as the bulk velocity increases relative to the thermal velocity, turbulence becomes more likely. Many people use the Reynold's number to analyse the stability of a fluid, and in general, we see increasing turbulence with increasing Reynold's number, however, the Reynold's number alone is not a true measure of the stability of a fluid, and care must be taken when it is used as one.
Boundary layer effects
The boundary layer immediately adjacent to a solid surface at the edge of a fluid does not move with respect to that surface. This is seen in the laminar flow through a pipe where the velocity of the flow decreases to zero towards teh edge of the pipe. Another example of this is the flow caused as a barge is dredged over the top of a still river or pond. The water at the boundary immediately above the river bottom stays fixed relative to the river bottom. The water immediately below the bottom of the barge stays fixed to the barge, and moves at the same velocity as the barge. If the speed of the barge is not too fast, the velocity of the water will change steadily between these two boundary conditions.

Pressure difference forces
Pressure is a measure of the motion of particles in a fluid. If a screen is placed in a fluid, the force per unit area caused by particles hitting the screen gives the pressure. For a fluid at uniform pressure, the number of particles hitting on either side of the screen would be the same, and the forces on either side would cancel. For a fluid in which there was a pressure differential from one side to the other, the pressure would be greater on one side, and that side would get a higher number of collisions, and would be pushed in the direction of lower pressure. In any fluid, a pressure difference leads to a force in the direction of decreasing pressure. The greater the pressure difference, the greater the force.Convection
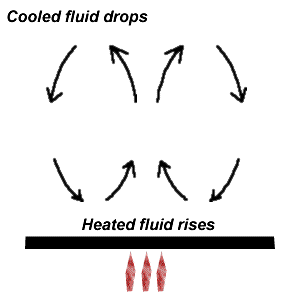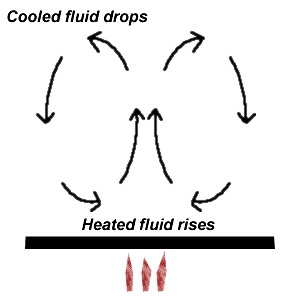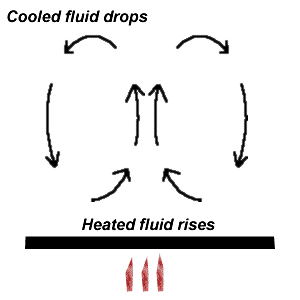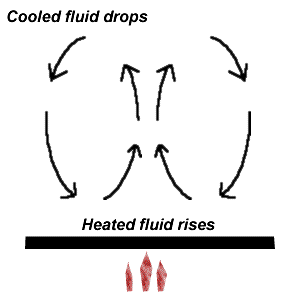
A parcel of gas heated at constant volume will experience an increase in pressure (see ideal gas law), and the pressure difference will cause the hotter air to rise.