|
This activity allows the user to step through the generation of a fractal made from deforming a line by bending it. This activity allows the user to step through the generation of a fractal made from deforming a line by bending it. The Koch Curve was studied by Helge von Koch in 1904. When considered in its snowflake form, (see below) the curve is infinitely long but surrounds finite area. To build the original Koch curve, start with a line segment 1 unit long. (Iteration 0, or the initiator) Replace each line segment with the following generator:

Note that we are really taking the original line segment and replacing it with four new segments, each 1/3 the length of the original. Repeat this process on all line segments. Stages 0, 1, and 2 are shown below.
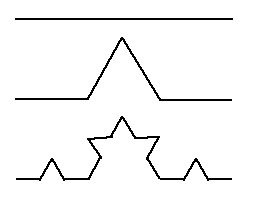
The limit curve of this process is the Koch curve. It has infinite length. Notice also that another feature that results from the iterative process is that of self-similarity, i.e., if we magnify or "zoom in on" part of the Koch curve, we see copies of itself. The idea of the Koch curve was extended to the Koch "Snowflake" by applying the same generator to all three sides of an equilateral triangle; below are the first 4 iterations.
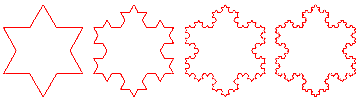
In the limit, the snowflake has infinite perimeter and finite area. Class Resources
|

