Example 3: Methyl Cyanide

Z-Matrices

Students

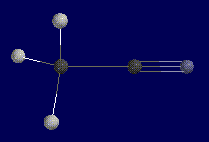This is Methyl Cyanide. Notice the pyrimidal shape of the three hydrogens and linear geometry of the two carbons and nitrogen. These three atoms form a 180 degree angle and will pose a problem when calculating the z-matrix.

There are two ways to build this z-matrix;

Using a Dummy Atom - (The preferred method)

Ignoring a connecting atom

Using a Dummy Atom:

Here is the numbered molecule. Use this as a reference when following along in the example. Notice that the black arrow means that atom H5 is coming out of the screen and towards you. The shaded arrow H4 is going into the monitor. The atom "X" is the dummy atom.

1. First we must decide which atom will be atom #1. We'll pick the carbon attached to the hydrogens and call it C1. Place this at the origin.

   C1

2. Next we must order the rest of the atoms. Designate the other carbon C2, the three hydrogens will be H3,H4,and H5, the dummy atom will be X6 and the nitrogen will be N7.
3. Now we must look at the C2 atom. Using our reference charts, we find the single bond length between two carbons equals, 1.54 angstroms.

   C1
   C2	1	1.54

4. Next look at atom H3. Its bond length to atom C1 equals 1.09 angstroms. The bond angle formed between the first three atoms equals 110.0 degrees.

   C1
   C2	1	1.54
   H3	1	1.09	2	110.0

5. Next we look at atom H4. Its bond length with atom C1 equals 1.09 angstroms. Its bond angle with atoms C1 and C2 equals 110.0 degrees. Its dihedral angle with atoms C1,C2,H3 equals 120.0 degrees.

   C1
   C2	1	1.54
   H3	1	1.09	2	110.0
   H4	1	1.09	2	110.0	3	120.0

6. Atom H5 is almost the same as atom H4 since their bond angles and bond lengths are identical. However, their dihedral angles are the negatives of each other since the atoms point in opposite directions. The new z-matrix is as follows:

   C1
   C2	1	1.54
   H3	1	1.09	2	110.0
   H4	1	1.09	2	110.0	3	120.0
   H5	1	1.09	2	110.0	3	-120.0

7. Now, all we have left is the nitrogen. The nitrogen atom poses problems because it forms a 180 degree angle with the two carbons. This angle cannot be computed be many computer programs. So, scientists have learned to get around this problem by creating a "dummy atom." By placing a make-believe atom between the first carbon and the nitrogen, you break up the 180 degree angle into two 90 degree angles. Now you can solve the z-matrix. The X6 atom (the "X" atom) is given an arbitrary bond length of 1.00 angstroms. It forms a 90 degree bond angle with the atom C1. We will say that the dummy atom forms a 0.0 degree dihedral angle with atoms C1,C2,H3 in order to preserve the 180 degree angle for the nitrogen. The z-matrix is as follows:

   C1
   C2	1	1.54
   H3	1	1.09	2	110.0
   H4	1	1.09	2	110.0	3	120.0
   H5	1	1.09	2	110.0	3	-120.0
   X6	2	1.00	1	90.0	3	0.0

8. Finally, we can identify the nitrogen atom (atom N7). We know that it creates a triple bond with the carbon of length 1.16 angstroms. It forms a 90 degree angle with atoms C2 and X6. Finally, we designate its dihedral angle with atoms C1,C2,X6 as 180 degrees. This is the final z-matrix:

   C1
   C2	1	1.54
   H3	1	1.09	2	110.0
   H4	1	1.09	2	110.0	3	120.0
   H5	1	1.09	2	110.0	3	-120.0
   X6	2	1.00	1	90.0	3	0.0
   N7	2	1.16	6	90.0	1	180.0

   Ignoring A Connecting Atom:

   This method is exactly like the method of using a dummy atom except for how we define the nitrogen atom.

   Here is the numbered molecule. Use this as a reference when following along in the example. Notice that the black arrow means that atom H5 is coming out of the screen and towards you. The shaded arrow H4 is going into the monitor.

   1. First we must decide which atom will be atom #1. We'll pick the carbon attached to the hydrogens and call it C1. Place this at the origin.

      C1

   2. Next we must order the rest of the atoms. Designate the other carbon C2, the three hydrogens will be H3,H4,and H5, and the nitrogen will be N6.
   3. Now we must look at the C2 atom. Using our reference charts, we find the single bond length between two carbons equals, 1.54 angstroms.

      C1
      C2	1	1.54

   4. Next look at atom H3. Its bond length to atom C1 equals 1.09 angstroms. The bond angle formed between the first three atoms equals 110.0 degrees.

      C1
      C2	1	1.54
      H3	1	1.09	2	110.0

   5. Next we look at atom H4. Its bond length with atom C1 equals 1.09 angstroms. Its bond angle with atoms C1 and C2 equals 110.0 degrees. Its dihedral angle with atoms C1,C2,H3 equals 120.0 degrees.

      C1
      C2	1	1.54
      H3	1	1.09	2	110.0
      H4	1	1.09	2	110.0	3	120.0

   6. Atom H5 is almost the same as atom H4 since their bond angles and bond lengths are identical. However, their dihedral angles are the negatives of each other since the atoms point in opposite directions. The new z-matrix is as follows:

      C1
      C2	1	1.54
      H3	1	1.09	2	110.0
      H4	1	1.09	2	110.0	3	120.0
      H5	1	1.09	2	110.0	3	-120.0

   7. Now we are once again left with the problem of defining the nitrogen atom. The problem is with the bond angle of 180 degrees. One way to get around this, other than using dummy atoms, is to ignore the second carbon(atom C2). When you do this, you act as if there is one huge bond between atom C1 and atom N6. You find the bond length by summing the bond length of the two carbon single bond and the carbon-nitrogen triple bond. This gives you 1.54 angstroms +1.16 angstroms = 2.70 angstroms.
   8. Next you look at the bond angle between atoms N6, C1, and H3. This is equal to 110.0 degrees. (When finding this, remember to treat the bond between C1 and N6 as a single bond.)
   9. The only thing left is the dihedral angle. However, this method does not allow for you to assign this angle. We say that it is undefined. Thus, you enter a dihedral angle equal to 0.00 degrees in reference to atom C2. Now your final z-matrix should look like this:

      C1
      C2	1	1.54
      H3	1	1.09	2	110.0
      H4	1	1.09	2	110.0	3	120.0
      H5	1	1.09	2	110.0	3	-120.0
      N6	1	2.70	3	110.0	2	0.00

      Back