|
Student: In the Tessellation activity, the same shape is repeated over and over to make the pattern. Isn't this a type of symmetry? Mentor: Yes. There are many symmetries in tessellations. However, you need to be careful that you don't confuse line symmetry with the type of symmetries that we find in the plane of a tessellation. Student: I've noticed that sometimes you can find a line of symmetry for the whole pattern, but sometimes you can't. Does that mean that some tessellations aren't symmetric?
Mentor: Before we answer that question let's talk more about symmetry. Can you tell me what you mean by symmetric? Student:: I think a figure is symmetric when a line can divide the figure into two congruent halves. A butterfly is an example. If I draw a line down the center of the butteryfly's body, each half of the butterfly looks the same, like a mirror reflection. Mentor: That's right. What you are describing is called line symmetry. A more precise definition is that if you draw a line of symmetry, each point on one side of the line has a corresponding point on the opposite side of the line. If you connect these two points, that line is perpendicular to the line of symmetry. So, you are right, some tessellations don't have a line of symmetry:
 When we are talking about an infinite plane, we refer to the symmetries we find as plane symmetries or geometric transformations. If this tessellation did have a line of symmetry, we would refer to it as a reflection. Here is an example:
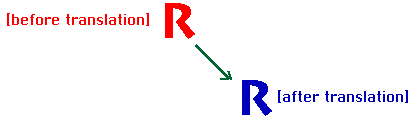
  Can you describe the characteristics of a reflection? Student: A reflection is flipping a figure across a line and making a mirror image. Mentor: That's right. All reflections have mirror lines. There are three other types of transformations in a plane. They are all transformations that move a pattern in a way that the pattern still matches the original pattern exactly. Let's look for the other three types. What other movement can we make to this pattern so that the pattern's appearance doesn't change? Student:We could slide the whole pattern sideways. Mentor: This kind of symmetry is called a translation. All translations have a direction and a distance. Can you make a tessellation that does not have translational symmetry? Student: Part of the definition of a tessellation is that it is a repeating pattern. So, I think all tessellations have translational symmetry! 
Mentor: Good observation. In what other way can you transform the pattern? Student: I could spin the pattern around a point, or rotate the pattern. That transformation would leave the pattern unchanged.
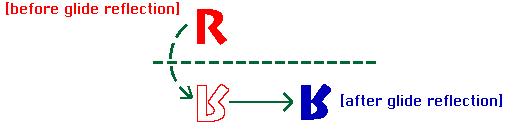
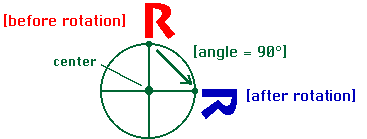 Mentor: This transformation is called rotation. Rotations always have a center, and an angle of rotation. Can you find one more way to transform the tessellation? Student: The only other thing I could do to the pattern would be to reflect it across a mirror line and then translate the pattern. But, isn't that two separate transformations? Mentor: Actually, that is one of the types of transformation and it is called a glide reflection. This is the only type of transformation that involves two steps: a reflection with a translation along the mirror line. Glide reflections are a separate type of transformation because some tessellations have glide reflections, but not reflections or translations. Here is an example:
Now, see if you can make tessellations with different combinations of transformations.

Please direct questions and comments about this project to Addison-Wesley math@aw.com © Copyright 1997-2000 The Shodor Education Foundation, Inc. © Copyright 2000 Addison-Wesley. All rights reserved. |