|
Student: So now I know all about building functions with variables! This isn't so bad! Mentor: Well, what you have actually learned so far is what very simple one operation functions are like. This is a very small part of the whole picture. The next thing we need to see is how certain situations require multiple step functions. Here's a picture:
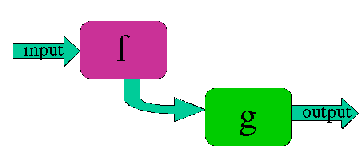 Student: So I put a number in the function named f and whatever comes out goes right into the function named g? Mentor: Yes! Try this example: g: y = 3 * x Student: OK; If I start with x = 2, putting it into f gives 2 + 1 = 3. Then I put 3 into g, which gives 9. So I say 9 for an answer?? Mentor: That's right! Student: That's easy! It's not any harder than doing one function. Mentor: That is true. Now, if you know what the output from the first equation is going to be you can combine the two equations. This is called composing functions or composition of functions. Student: So we could just write y = x + 1 * 3Mentor: Sort of. We need to be a little careful here, though, so that the person using the function knows to add first and then multiply. Mathematicians realized a long time ago (in the fifteenth century as algebra was being used more and more) that there needed to be rules about how to write anything with more than one operation so that there would be no confusion or argument. A standard evolved for the order of operations, which we still follow today:
Next comes multiplications and divisions in any order Save all additions and subtractions for last Unless, of course, parentheses are used - do that stuff first! Student: So the way I wrote it is wrong? I need to write it as y = (x + 1) * 3Mentor: Yes. You can also write the same thing these other ways:
Can you tell me why each of these is the same as out original two functions? Student: Well, each one gives the same output for 3 as an input. Mentor: That's true, but we have seen functions that are different for some numbers and the same for others. For example, y = x + 6 and y = 3 * x both give 9 as an output when 3 is the input. Can you explain it another way? Student: Well, the first two say that x+1 needs to be done first since it is in parentheses, and them we multiply by 3 since that is the only thing left to do. They are different only because one has the times symbol and the other doesn't. The second two are different from the first two. They have used the rule that says we distribute the times across the plus. Mentor: Good. So they are all the same because they are rearrangements that follow arithmetic rules like
Student: So the same function can have different forms? Mentor: Exactly - and when we allow more complicated things like lots more than just one or two operations and include exponentiation in the list, checking that two functions are equivalent gets more challenging. This is one of the interesting problems in algebra. Try some more composite functions yourself!

Please direct questions and comments about this project to Addison-Wesley math@aw.com © Copyright 1997-2001 The Shodor Education Foundation, Inc. © Copyright 2001 Addison-Wesley. All rights reserved. |