Student: I know what dimensions are:

• Points have dimension 0
• Lines have dimension 1
• Plane figures like squares have dimension 2
• Solid volumes like cubes have dimension 3

Mentor: Good! What can we learn from these statements? Let's start with a line, since points are not so interesting as far as fractals go.

Lines have length, but no width or height, so we can measure them in 1 dimension only. Because of this we say:

Consider the line segment below:

Now let's build similar line segments at a smaller scale. We'll use a scale factor of 4 (the large segment is 4 times longer than the small ones).

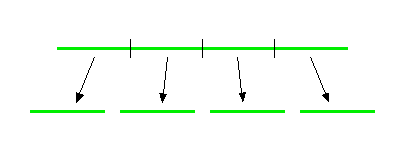Notice that we can get 4 "self-similar" line segments out of the original line segment at this scale factor. So: Dimension = 1, Scale = 4, and Number of self-similar objects = 4.

You try this for a square (plane figure).

Student: Ok: The Euclidean dimension of a square is 2 because we can measure the length and the height, but there's no thickness. Consider the square below:

Now let's build similar squares at a smaller scale. We'll use a scale factor of 3 (the side of the large square is 3 times longer than the small ones).

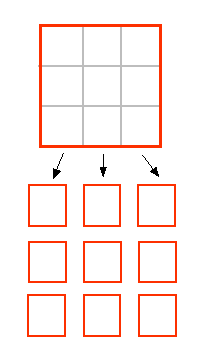Notice that we can get 9 "self-similar" squares out of the original square at this scale factor. So: Dimension = 2, Scale = 3, and Number of self-similar objects = 9.

Mentor: Let's do a cube (solid) together: The Euclidean dimension of a cube is 3 since we can measure the length, width and height. Consider the cube below:

Now let's build similar cubes at a smaller scale. We'll use a scale factor of 2 (the side of the large cube is 2 times longer than the small ones).

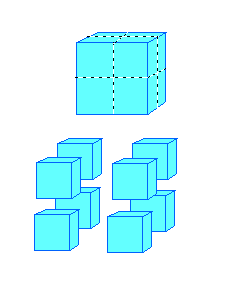Notice that we can get 8 "self-similar" cubes out of the original cube at this scale factor. So: Dimension = 3, Scale = 2, and Number of self-similar objects = 8.

Mentor: What pattern do you see here?

Student: Dimension, Scale and Number of copies seems to follow:

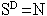Mentor: Good! Fractals are objects that have fractional dimensions! To see this we need to learn about finding D when we know S and N -- this is not trivial since D is in the exponent. We need to talk about Exponents and Logarithms.

Please direct questions and comments about this project to Addison-Wesley math@aw.com
© Copyright 1997-2001 The Shodor Education Foundation, Inc.
© Copyright 2001 Addison-Wesley. All rights reserved.