One of the key considerations in choice of a computing platform and a software tool is the size of the problem and the number of calculations needed to be done. The problem described in this case study is, as you might suspect, requires little in the way of computing power and software, so we choose the least restrictive/least expensive environment we can find. Since we're dealing here with a system of three ordinary first-order differentials (ODEs), with a system dynamics approach, I would choose to use a system dynamics modeler known as STELLA from High Performance Systems. STELLA runs on both Macintosh and PC Windows computer, and is designed to handle systems of differential equations with the Euler's and Runge-Kutta numerical methods as a part of the software. The interface is graphical -- to build a model a researcher selects an appropriate icon to represent the various mathematical components of the system. The software allows for simple creation of run-time graphs and data tables, both of which can be exported to other packages, including high-end visualization packages. The Chesapeake Bay Labs in Solomons Island MD have recently created a translator for STELLA that allows one to do spatial modeling with STELLA, with the generation of code in the C programming language that can be run on parallel architectures.
Explaining the Model
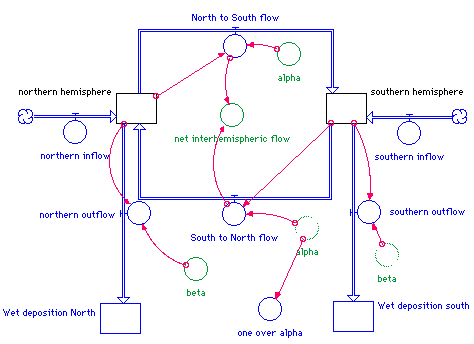
This model shows all the variables that can influence a process in the transport of atmospheric hemisphere. In Stella the boxes are called stocks and used for measuring the amount of that constant. The round circles are called converters and hold numbers that don't change like rates. Flows are circles with arrows connecting them to two stocks. These show how the pollutants move from one place to another.
Using the Model :
The question being asked by this model is:
For different inputs (amount of ethane, EN and ES, emitted by the nasty polluters !), how long does it take (in years) until the stuff emitted in the North stays there and the stuff emitted in the South stays there -- in other words, how long does it take for a steady-state/equilibrium condition to be in effect?
|

